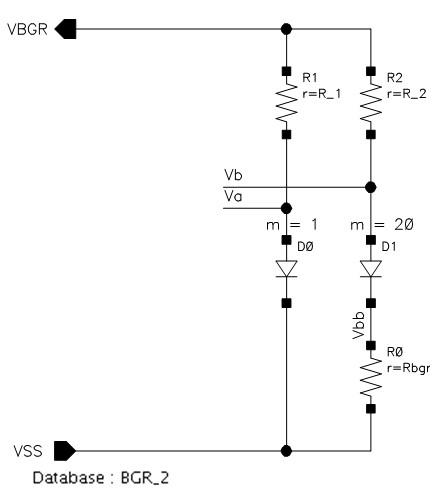
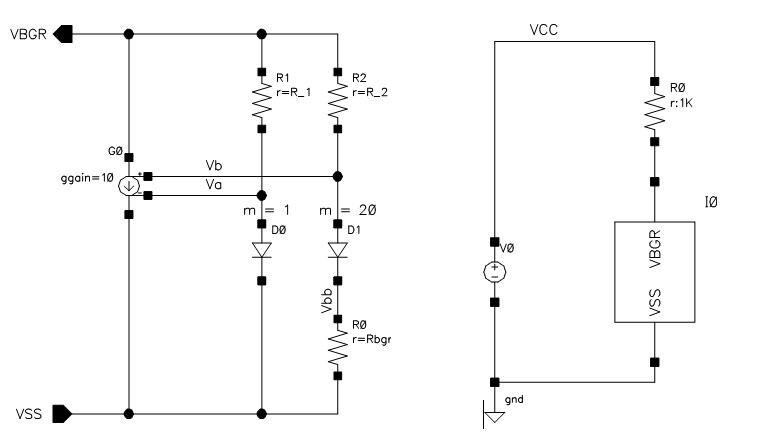
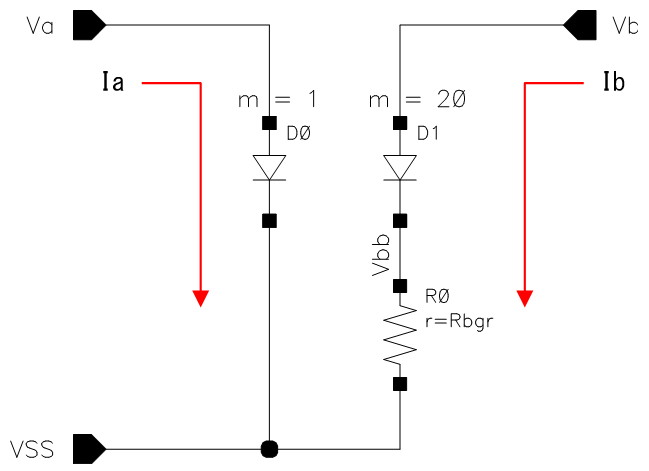
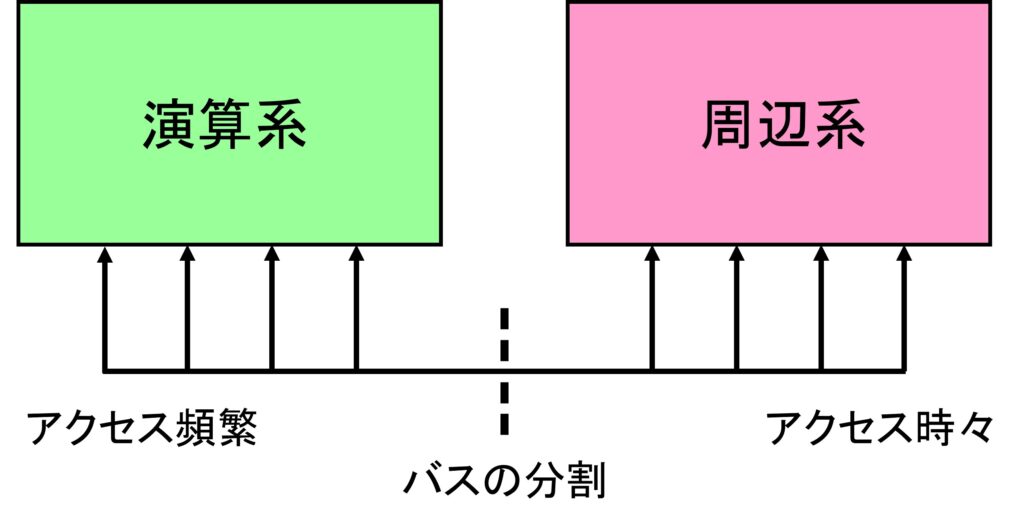
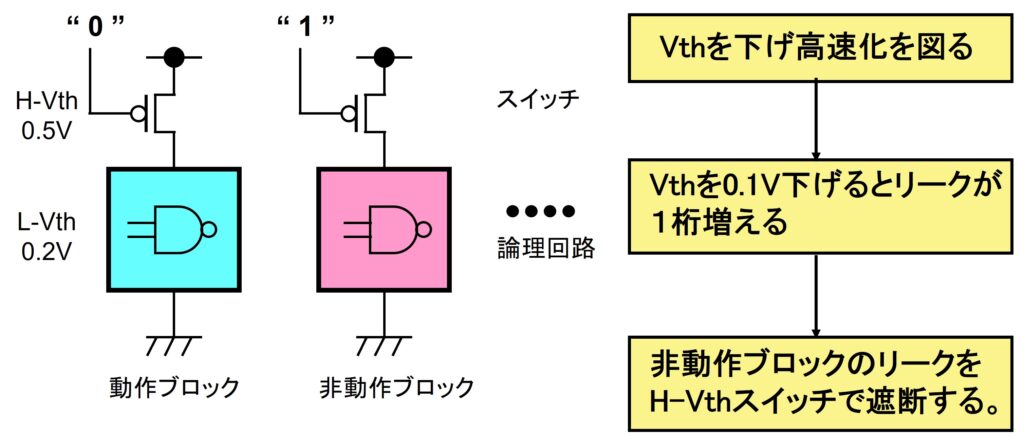
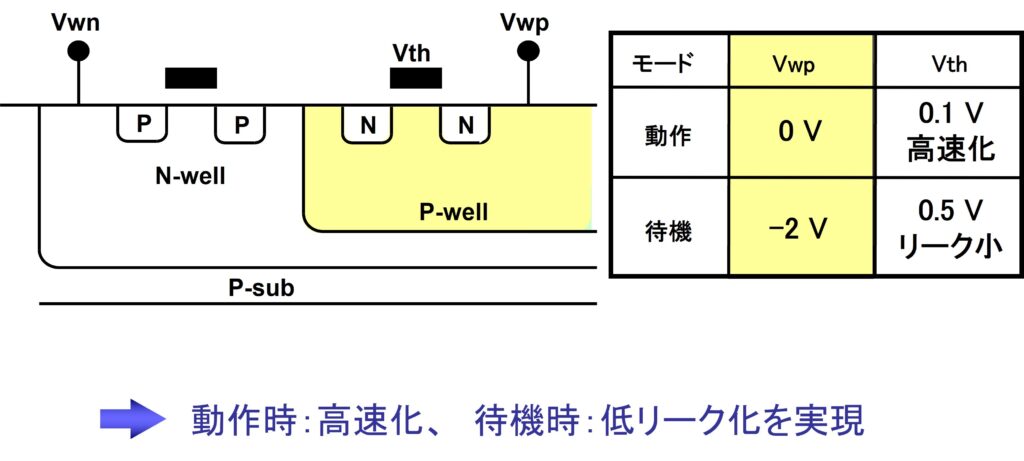
BGR(2) からの続きです。今日はBGR(Band Gap Reference)をその周辺回路も含めて紹介します。図1にBGR回路の基準部とアンプ部を示します。
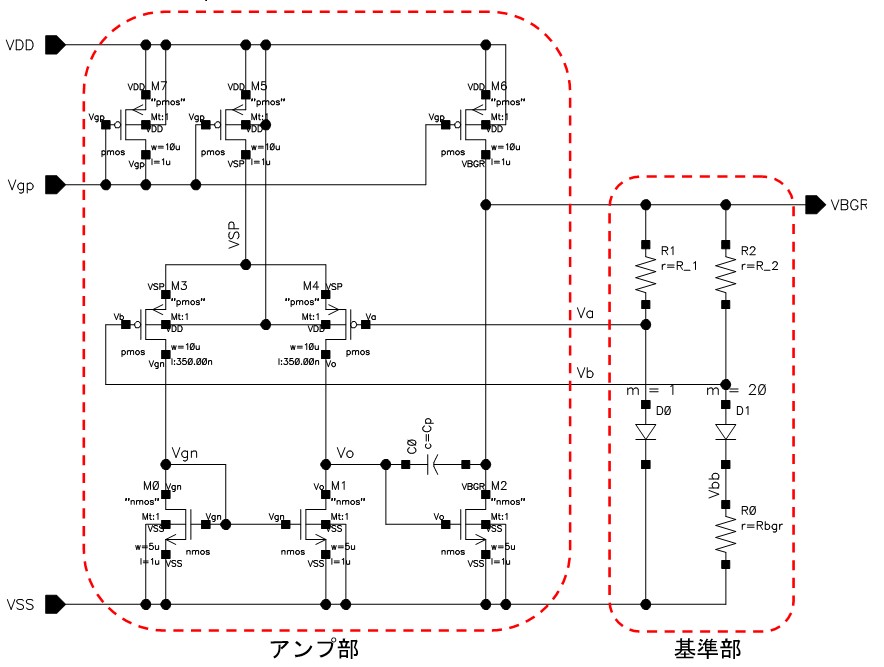
基準部は前回のBLOGで使ったものと同じで、アンプ部はVaとVbが等しくなるようにVBGRを制御します。
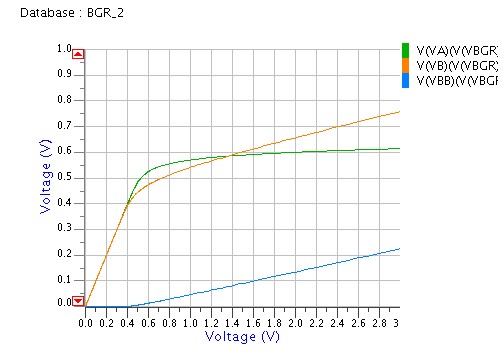
BGRの基準部の電位V1,Vbが約0.8VでGNDに近いので、電流源のスペースを確保しやすいPchを入力段を使うことが多いです。
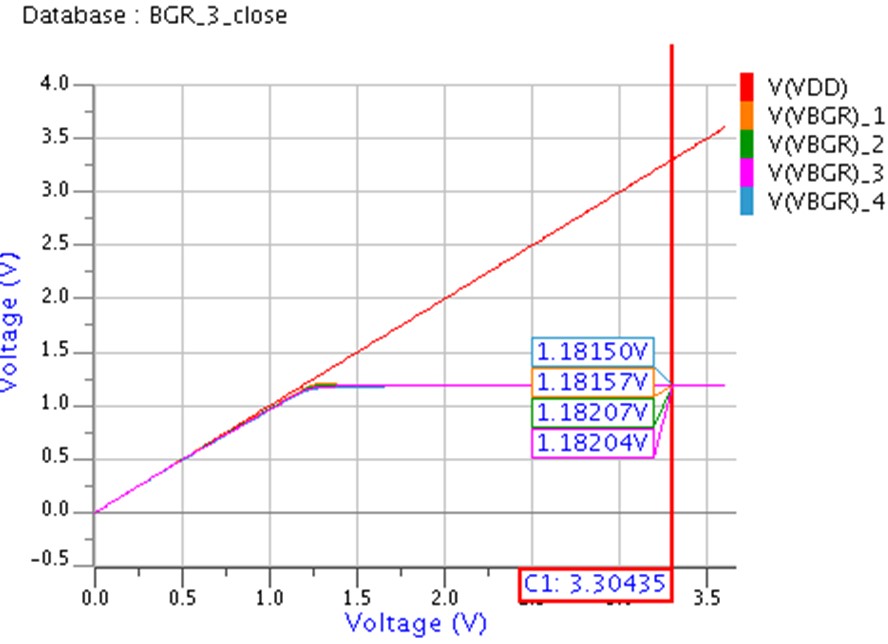
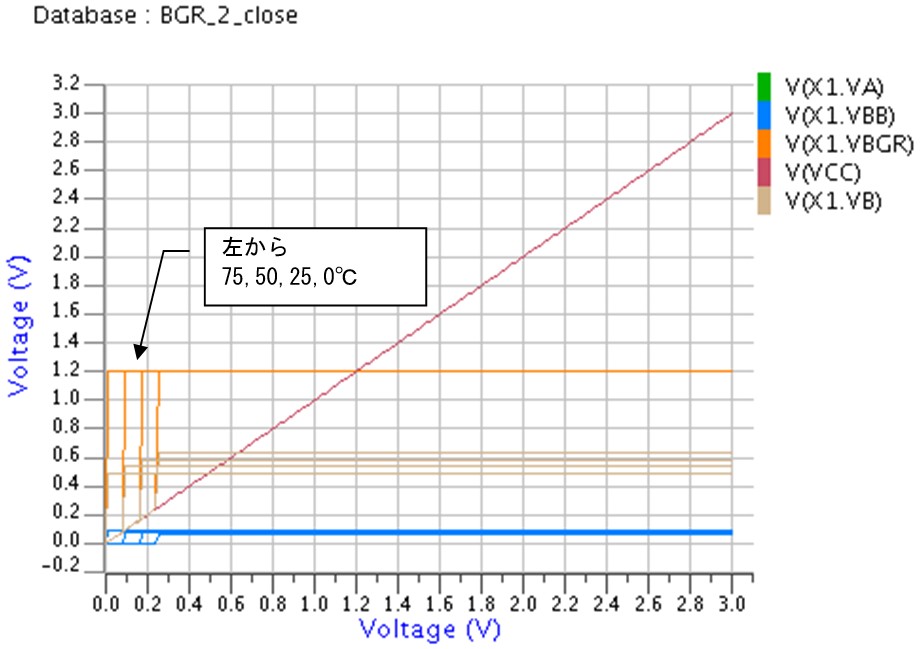
Vgp端子からGNDにむけて10uAの電流源をつけて、温度を0,25,50,75℃とパラメータにして、電源VDDを起動して時の様子です。
電源が変わっても、Vbgrはほとんど動いていません。
温度が0~75℃変わっても1.18207-1.1815=0.00057Vの変動なので・・・6.4ppm!
ちょっとよく出来すぎました(汗)
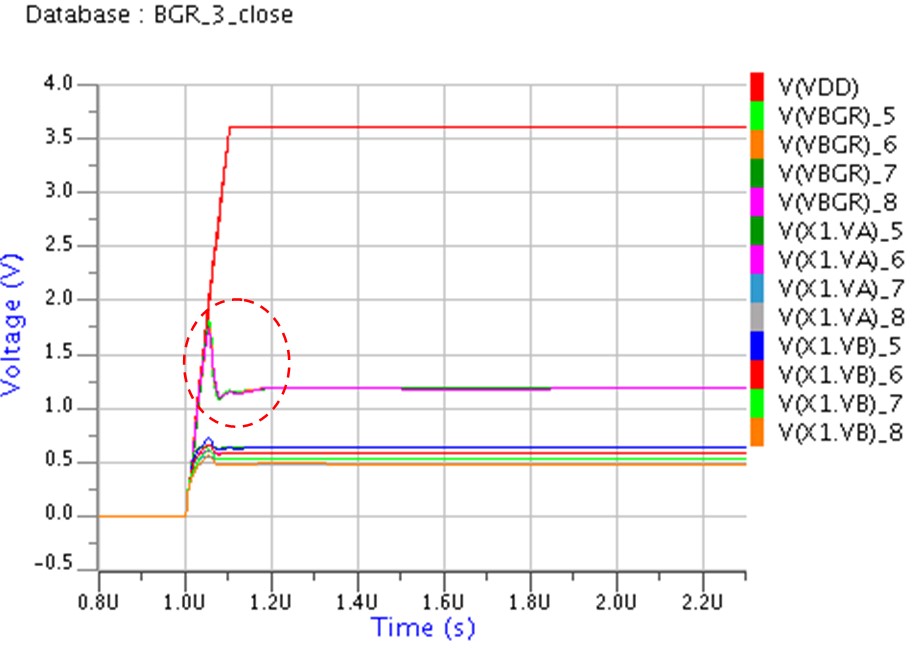
上の波形は、電源を0.1usecで起動したときのもので、丸印の所にリンギングが見えます。
このままでは発振してしまう可能性もありますので、アンプに位相補償用のコンデンサ(図 1のC0)を入れます。
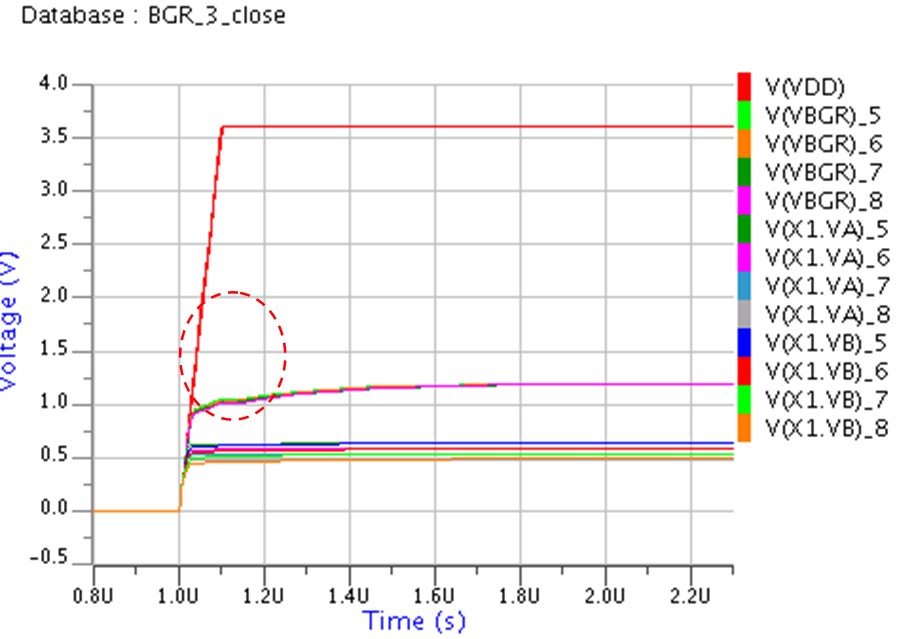
C0=2pFとした結果をが上の図になります。リンギングが解消されて安定して起動できていることがわかります。
BGR回路は負帰還回路なので、ループの安定度を確認しておく必要があります。
そのためにはClose LoopをOpenにして、一巡伝達特性を(ぞくにμβって言います)見る必要があるのですが、上のように電源起動の様子を見ることで簡易的にループが安定しているかを確認できます。
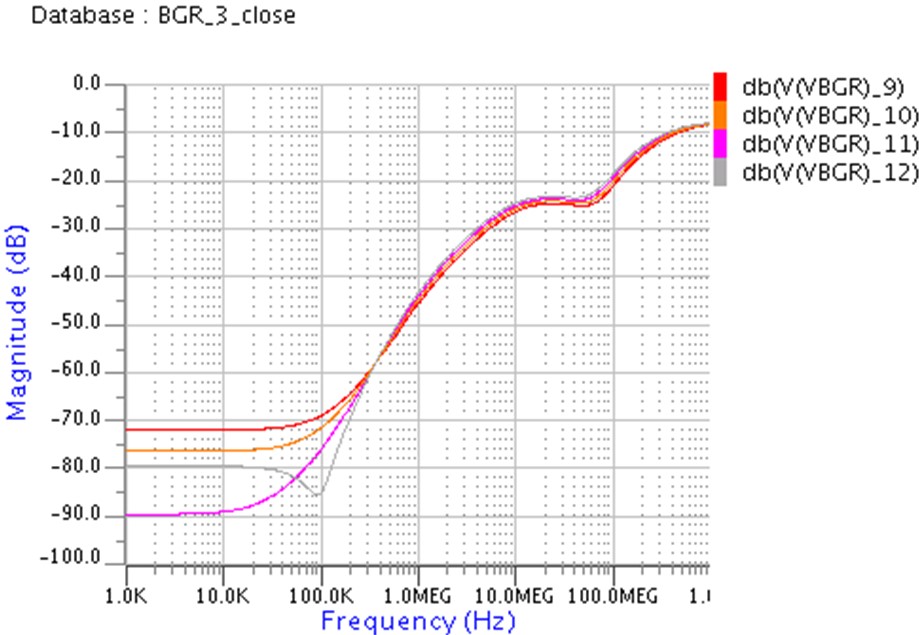
上の図はAC解析の結果です。VDDを信号源にして電源が揺すられた時に、VBGRがどれだけ揺すられるかを見ています。100KHzくらいまでは-70dBなので・・・1/3000に電源のゆれを小さくできていますが、周波数が高くなると徐々に電源の影響が出てきて、100MEGHzでは1/10にしか電源のゆれを圧縮できていません。
BGR出力にどのような性能を求めるのか、電源VDDがどのようなゆれ方をするのかに依りますが、場合によってはVBGR出力にコンデンサを追加する場合もあります。
これでBGR回路の紹介は終わりです、と言いたい所ですが重要な説明が抜けていました。
それは、“オフセット電圧の影響“です。
次回は、トランジスタのオフセット引き起こすBGR回路の問題と、その対策について紹介したいと思います。