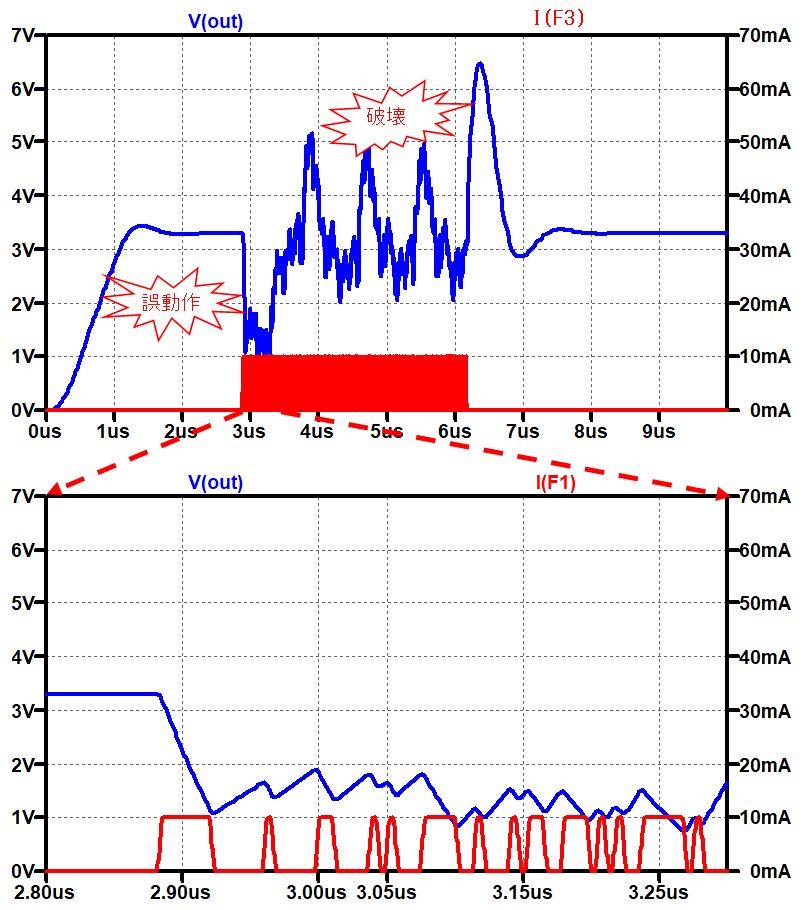
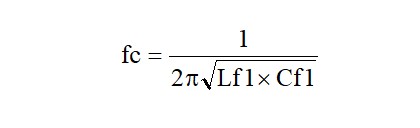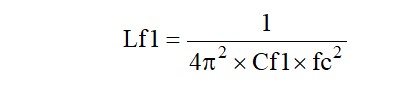電源フィルタの部品の寄生素子
寄生素子は必ず発生する
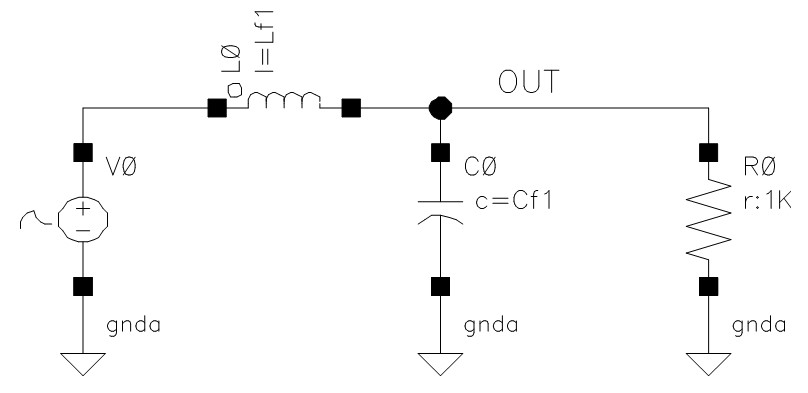
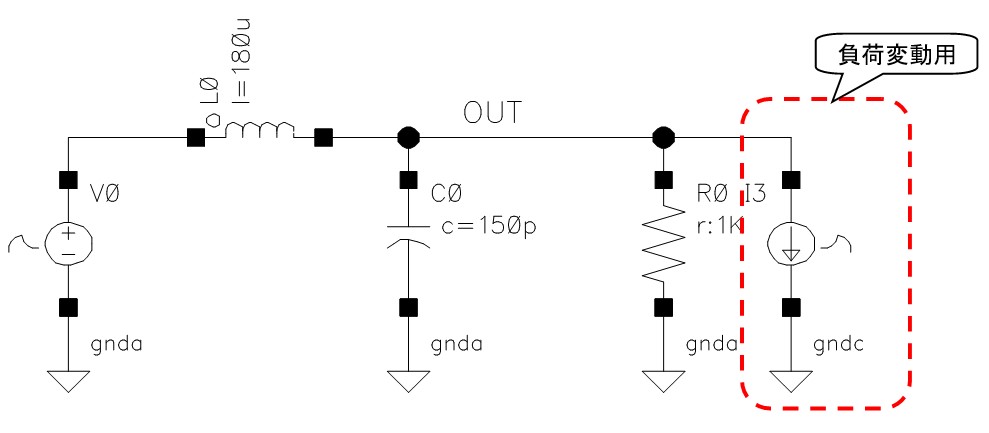
今回は電源フィルタを構成する部品の寄生素子分を含めた場合について紹介したいと思います。寄生素子とは、素子に寄生するものなので、出来れば無いほうが良いのですが、実際には必ず寄生素子が存在します。寄生素子はその物理的な構造やサイズなどから決まり、例えば、インダクタにはコイル以外に抵抗やコンデンサが寄生しています。
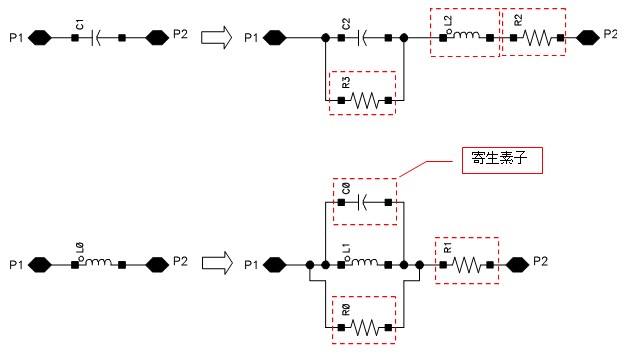
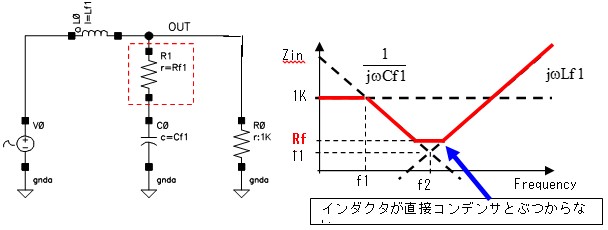
図 1
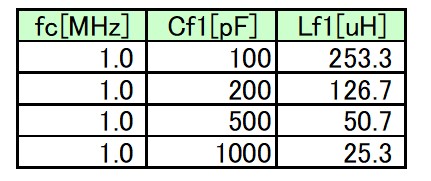
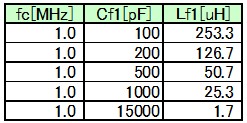
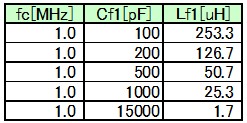
具体的な値は以下のような値をとります
Lf1=1.8uHの場合
R0=5800Ω
R1=0.4946Ω
C0=0.291pF
Cf1=15000pFの場合
R2=0.0462Ω
R3=10GΩ
L2=0.42nH
電源フィルタにおける寄生素子の影響
これらの寄生素子を考慮に入れるとインダクタやコンデンサの特性は次のように変化します。
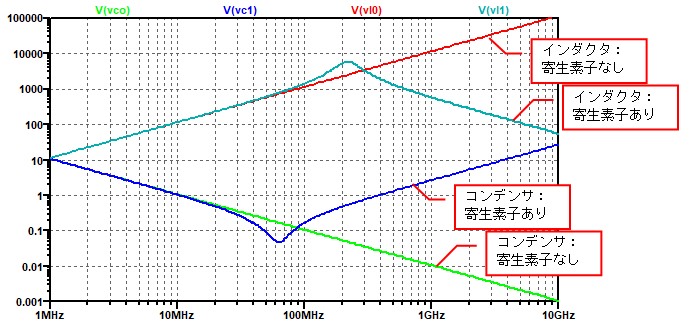
図 2
コンデンサは60MHzより高い周波数ではインダクタに変わり、インダクタは200MHzより高い周波数ではコンデンサに変わってしまっていることが分かります。
つまり、ある周波数(自己共振周波数などと呼びます)より高い周波数では、インダクタやコンデンサはもはや別の素子に変化していると言うことです。
高周波の寄生素子
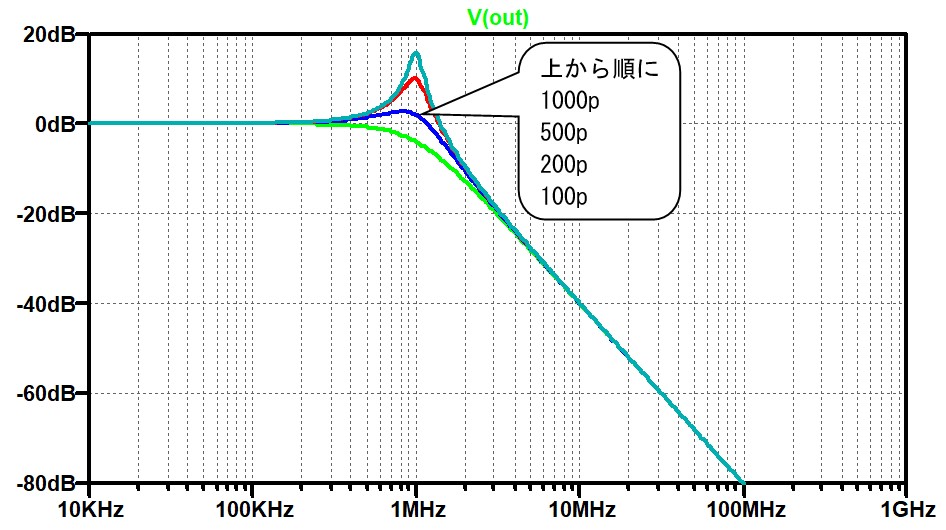
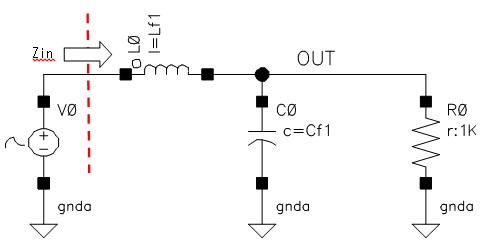
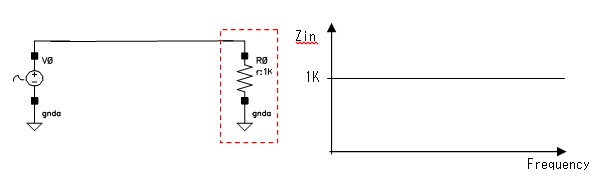
これらの寄生素子を使って電源フィルタの特性がどうなるかを調べてみました。
なお、使った定数は上のほうで使った値でLf1=1.8uH、Cf1=15000pF、Rf1=15Ωで、寄生素子を含みます。
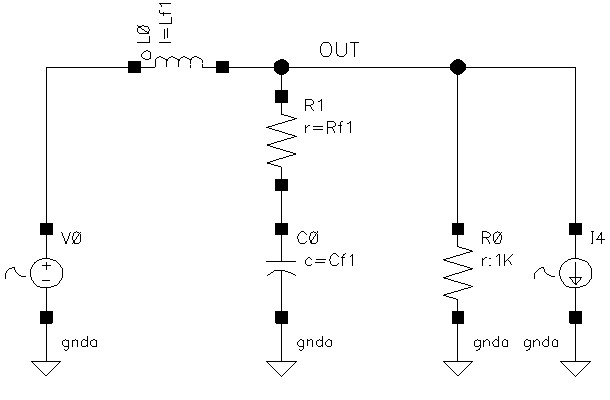
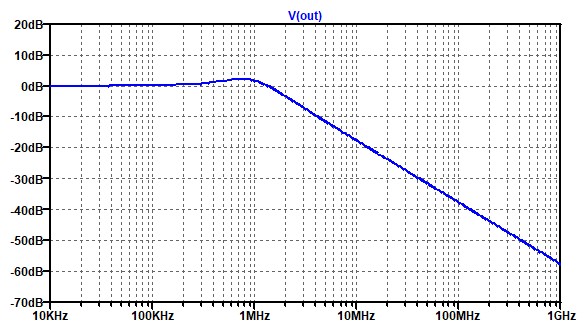
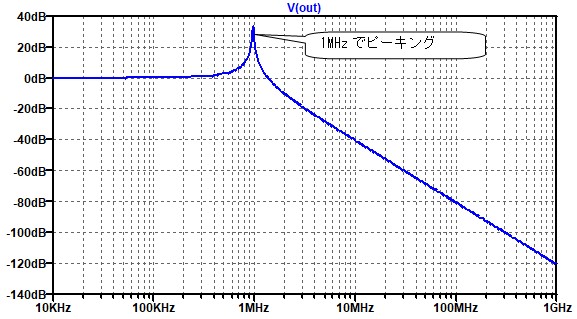
図 3
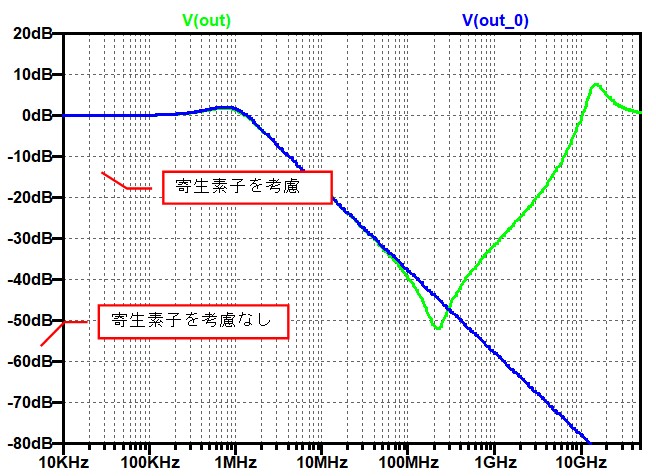
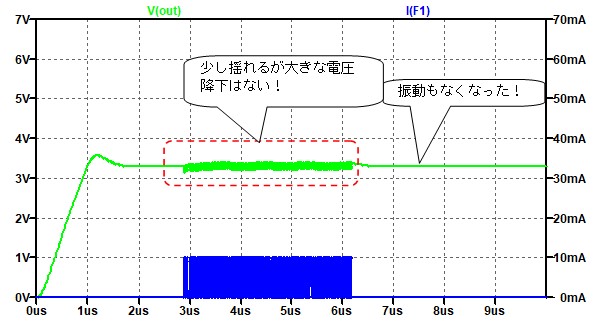
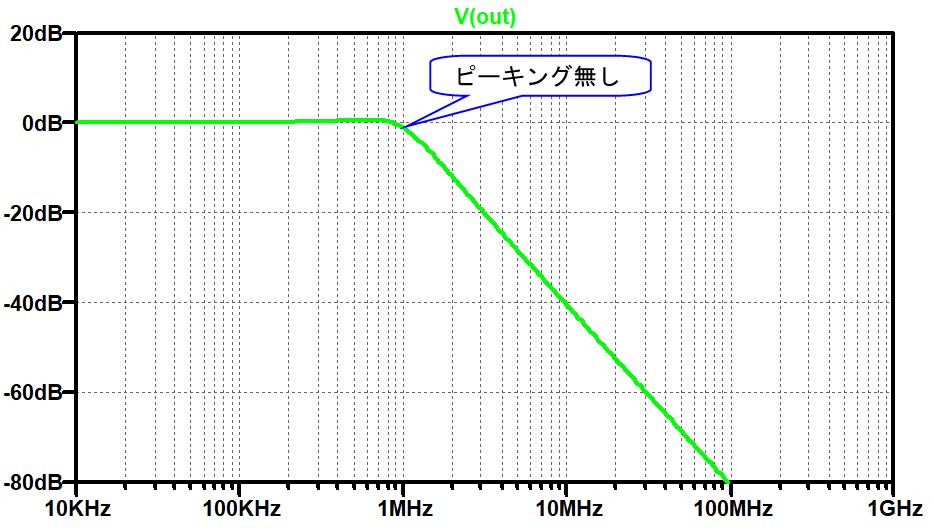
図 4
この結果を見ると、寄生素子の影響は100MHz以上で現れる事が分かります。つまり、寄生素子がない場合と比べると、電源雑音を除去する能力が悪くなり、雑音やリップルが回路側に入ってきてしまいます。このように高い周波数が電源から発生する事は少ないように思うのですが、実際に回路ではありえないとは言い切れません。例えば、同じボード上にRFのパワーアンプが搭載されている時などには、数GHzの雑音(と言うよりも信号成分)が電源経由で入り込む事が良くあります。
高周波の雑音を電源に加えてみる
もし、高周波の雑音が電源に加わったとしたらどうなるかを確認してみましょう。
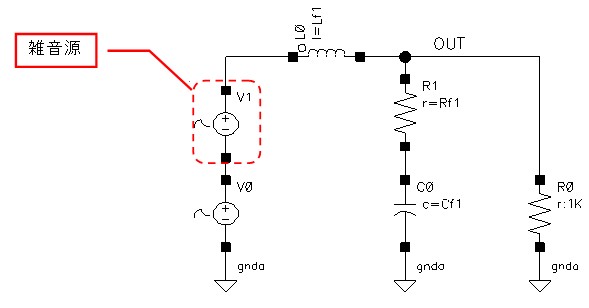
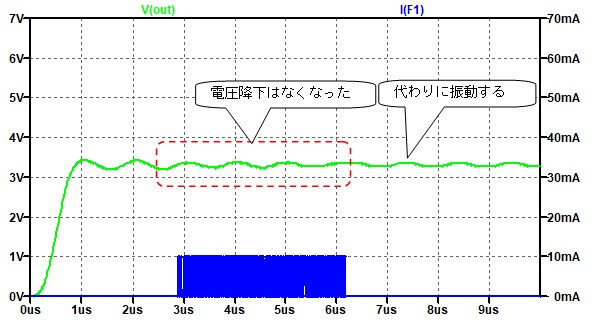
図 5
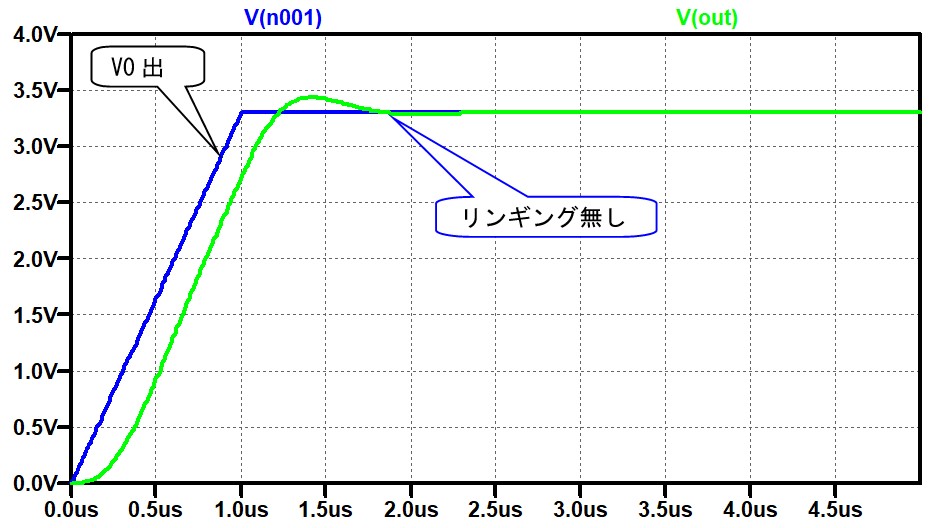
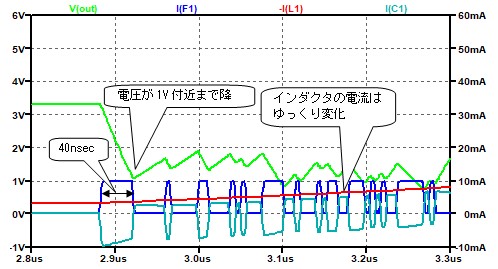
上の図のように雑音源(5GHz,2Vppの正弦波)が加味されたときの過渡解析は以下のようになります。
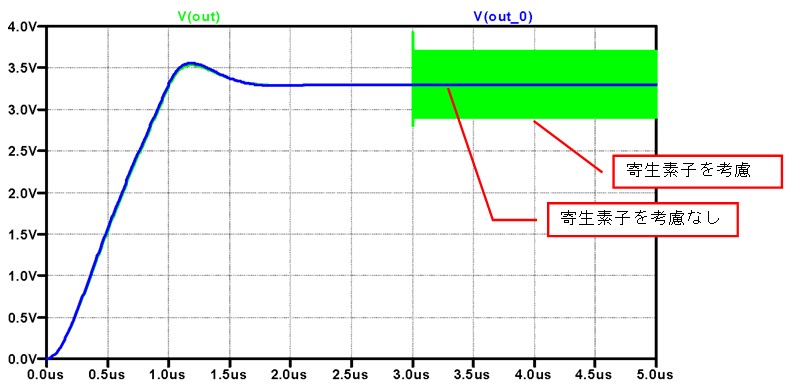
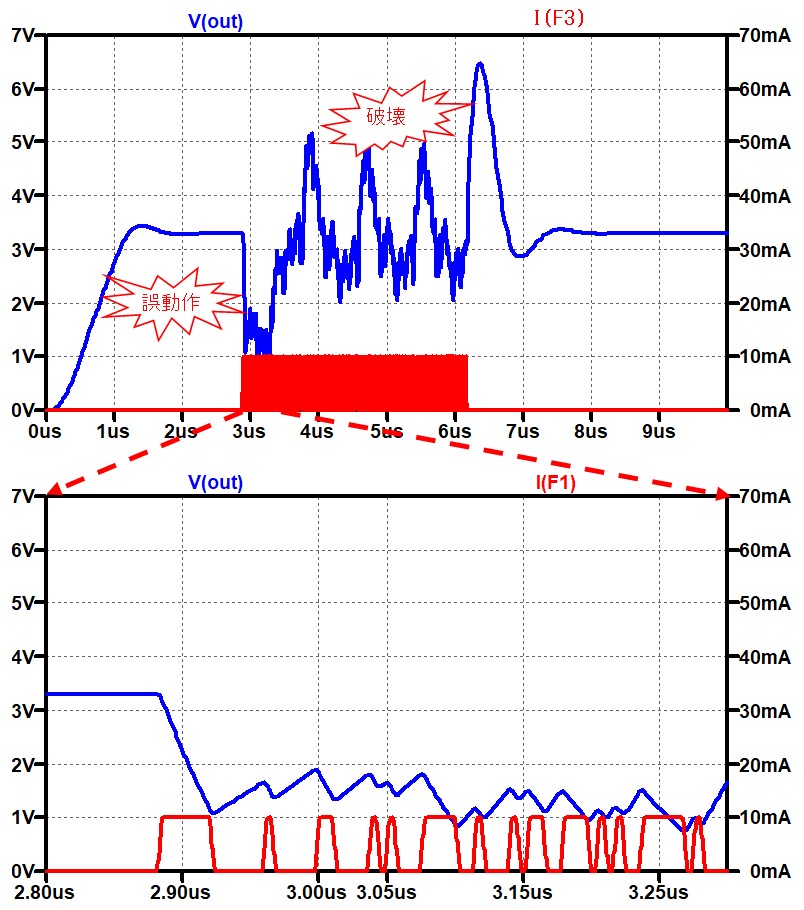
図 6
寄生素子を考慮していない回路では、電源に雑音は現れないのですが、寄生素子を考慮した計算では、雑音とした追加した5GHzの信号成分がまだ消えずに残っています。
ノイズの原因は結局電源フィルタということも良くある
今回は非常に大きな雑音源を印加して見やすくしていますが、実際に回路ではこのように大きな雑音が見て分かるように混入する事は比較的に少ないです。しかし、オシロでは見えないような小さな雑音でも感度の高いプリアンプが増幅してしまい、S/Nが悪くなってから初めて気が付く事もあります。その原因は追っかけていくと大半は電源フィルタの構成にたどり着きます。
“電源だからそんなに高い周波数成分は気にしなくても平気だろう”って考えがちです。しかし、高周波と低周波ある周波数で区別するものではなく、全部周波数特性として繋がっているので、”周波数が低いから大丈夫!”言った思い込みは危険です。(美斉津)
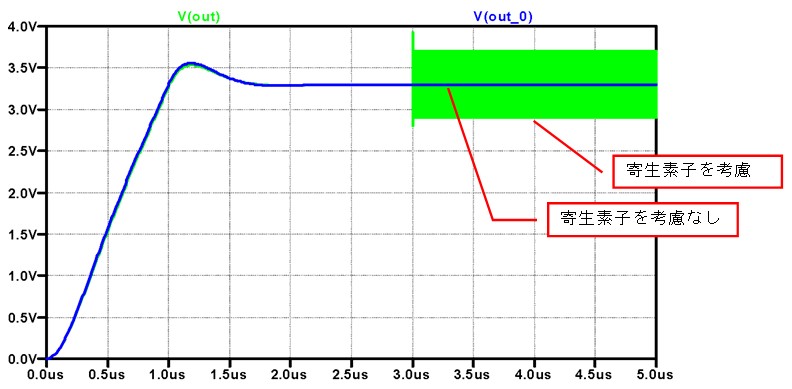
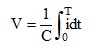




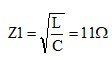 となります。
となります。