こんにちは!今日はAIモデル開発のデータ収集についてお話しします。
前回の記事はこちら
AIモデルの学習と評価には、どれだけのデータが集まるかが非常に重要です。成功するプロジェクトには、質の高い、大量かつ多様なデータが必要不可欠です。実際データはAIモデルそのものよりも重要だと言えます。
データ収集とアノテーションの重要性
データ収集やアノテーション(データラベリング)は、多くのリソースを必要とする手間のかかる作業です。そのため、効率的にデータ収集やアノテーションを行うために、使いやすいアプリケーションを活用したり、自動化、半自動化のプロセスを取り入れることが重要です。
データ収集とは?
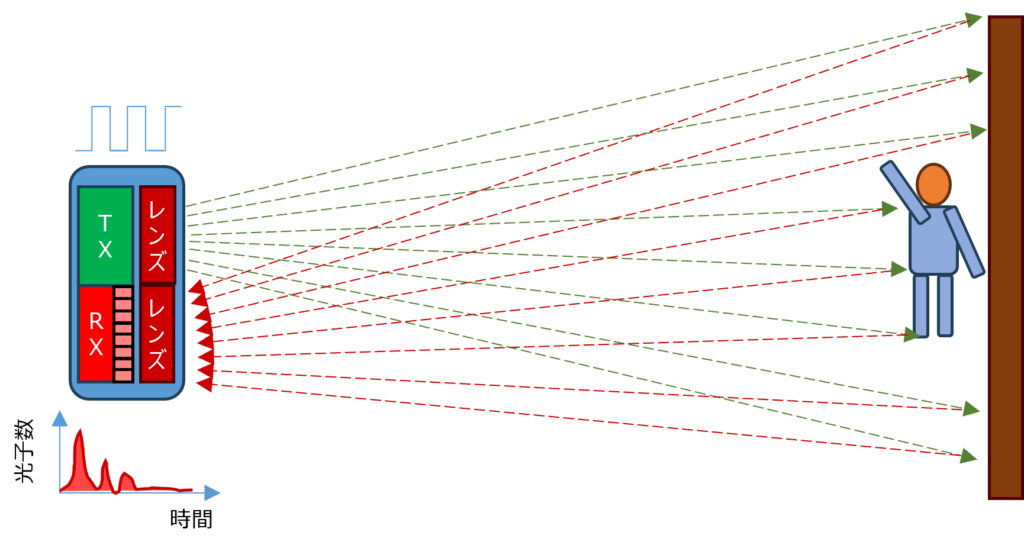
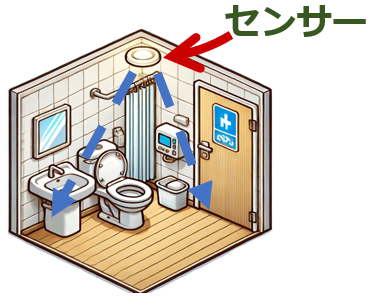
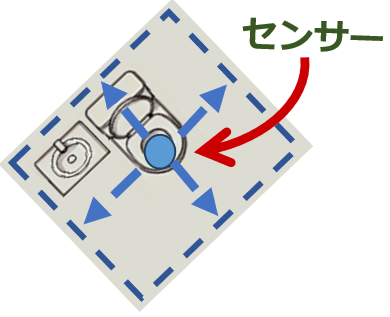
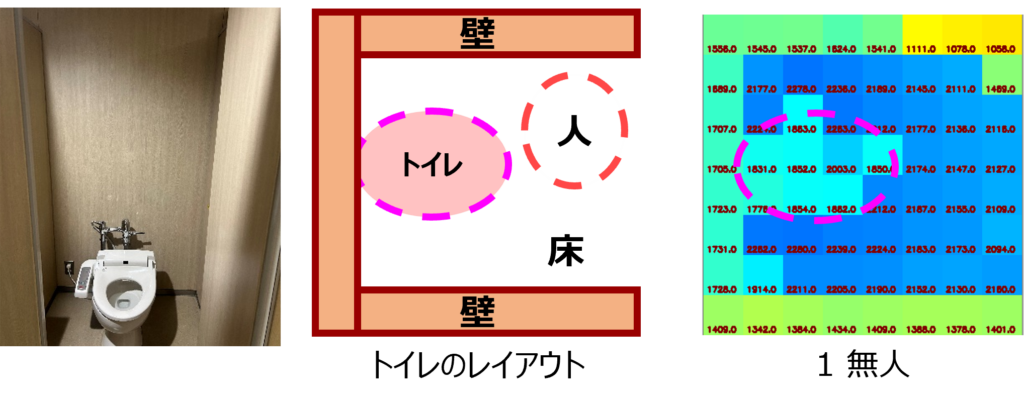
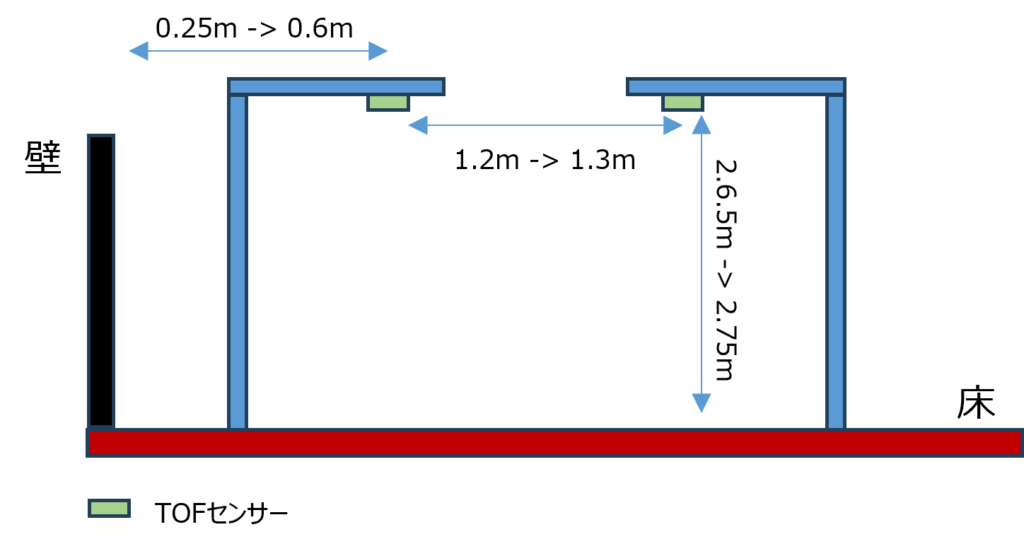
2024年のTOFセンサー PoCでは、2つのTOFセンサーを使ってデータを収集しました。6週間のプロジェクト期間中に、実質的には2週間分の測距データが収集されたのです。実際のトイレを長期間利用するのは難しかったため、工場内の一室を借りて、実際のトイレのレイアウトに合わせた測距データ収集用のトイレを設置しました。
データ収集においては、多様性が鍵となる要素です。具体的には以下のような点に配慮しました:
部屋のレイアウトやTOFセンサーの設置位置のバリエーション
数種類の台を使ってTOFセンサーの距離を変えたり、トイレの設備のバリエーション(便座の位置、タンクの有無など)を変えたりしてバリエーションを収集しました。
トイレのバリエーション


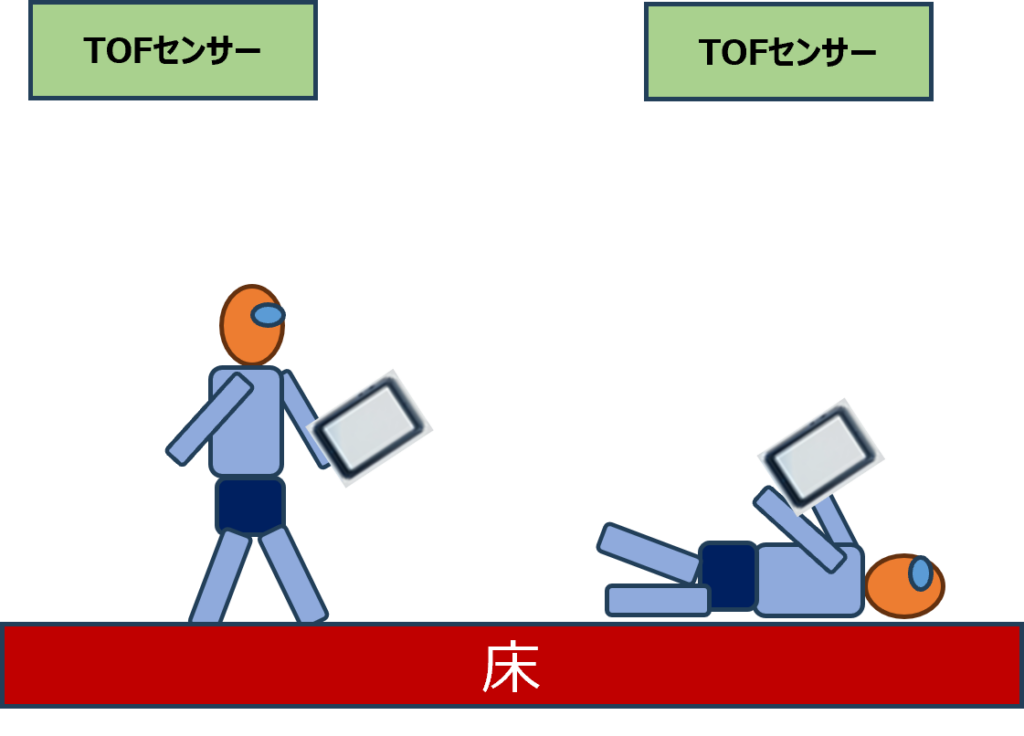
さらに、様々な人の姿勢や位置を含む測距データの多様性(体格や身長の違い、立っている・歩いている状態、異なる服装による影響など)を担保すべく、人との姿勢や人数のバリエーションを収集しました。
人間の測距データバリエーション
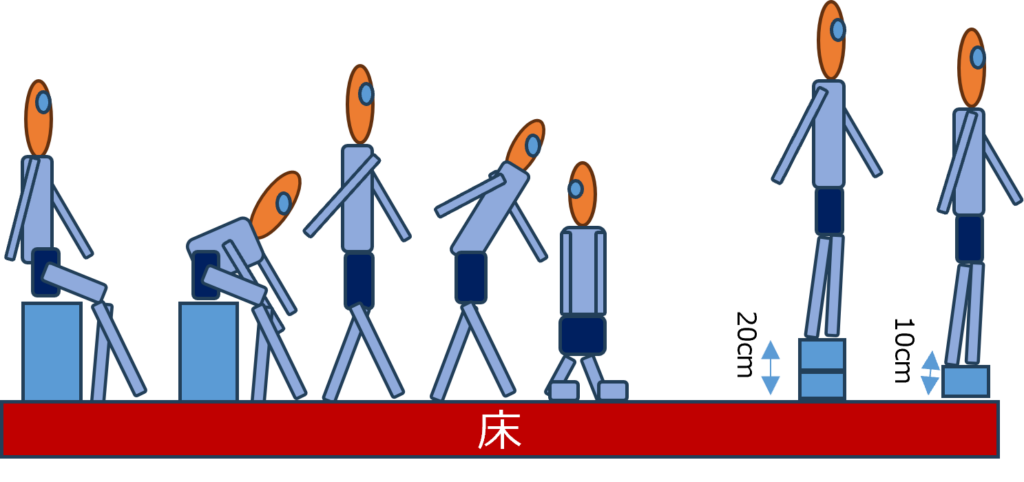
- 異なる体格や身長の人
- 154cm->181cm
- さまざまな姿勢や位置で立つ/歩く人
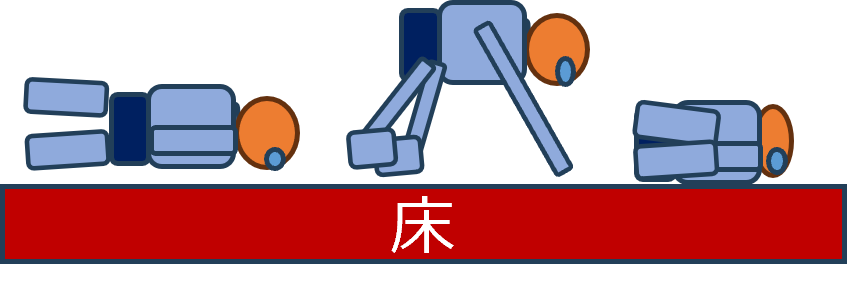
- 異なる形や位置での転倒
- 複数人の存在(2人いる時)
- 異なる服装の人(赤外線反射と吸収)
人間以外の測距データバリエーション

- 靴、ブロック、バッグ等が床に置かれた状態

アノテーションについて
データ収集とアノテーションは時間と人手を要する作業です。そこで、時間短縮を目指し、データ収集プロセスを設計しました。データの収集と解析を同時に実施できるように工夫しています。
アノテーションの入力方法
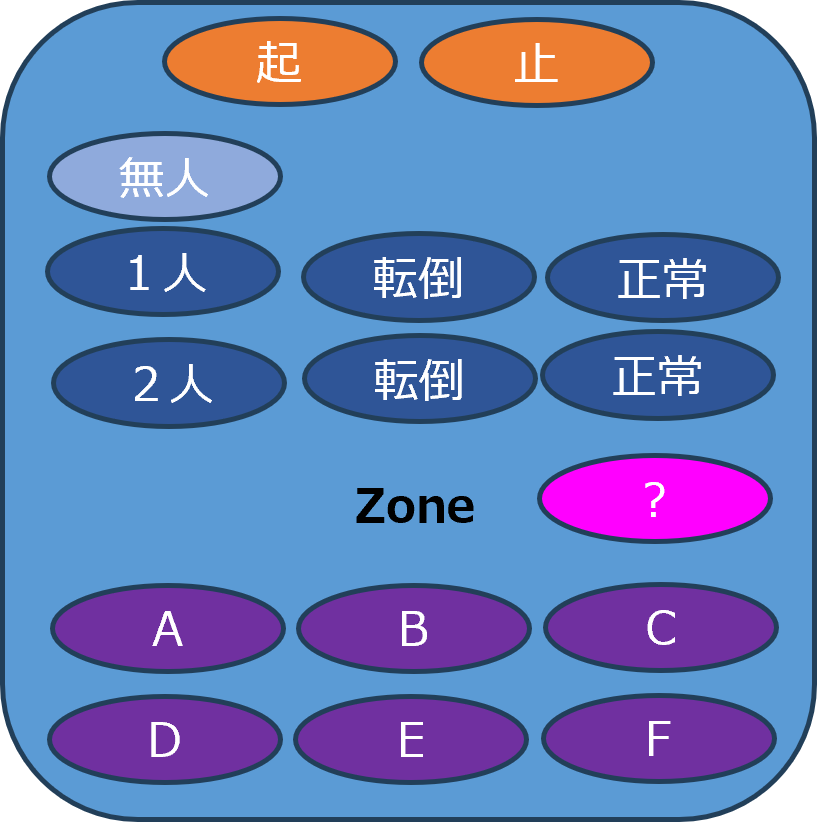
Bluetoothキーパッドを利用して、データ収集アプリケーションをリアルタイムで制御しました。これにより、ほとんどのデータ収集作業を一人で行うことが可能になり、2人分のデータ収集でも2人だけで対応できるようになりました。
データラベル設定
データラベルには以下の情報が含まれます。
- 人数
- 人の状態(転倒または正常)
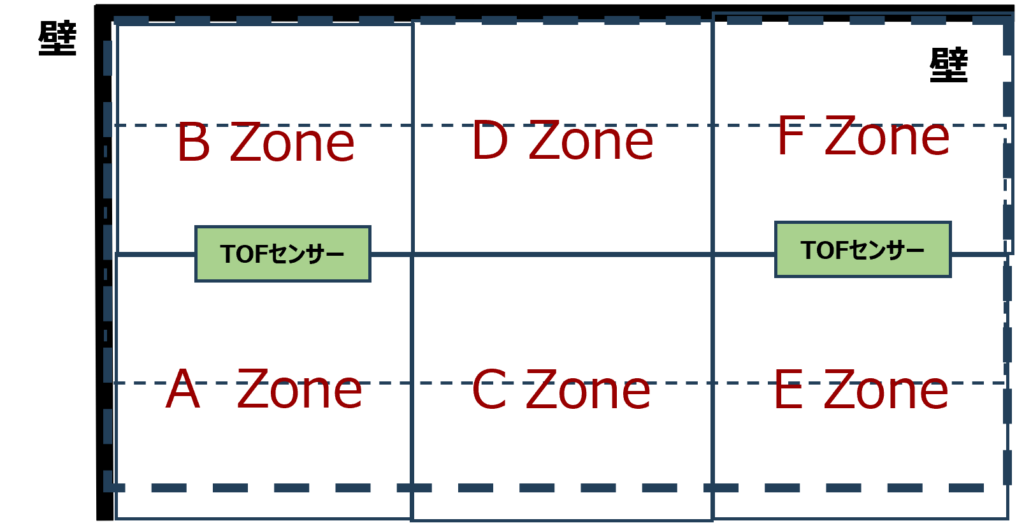
- 人が存在するエリア(ゾーン)
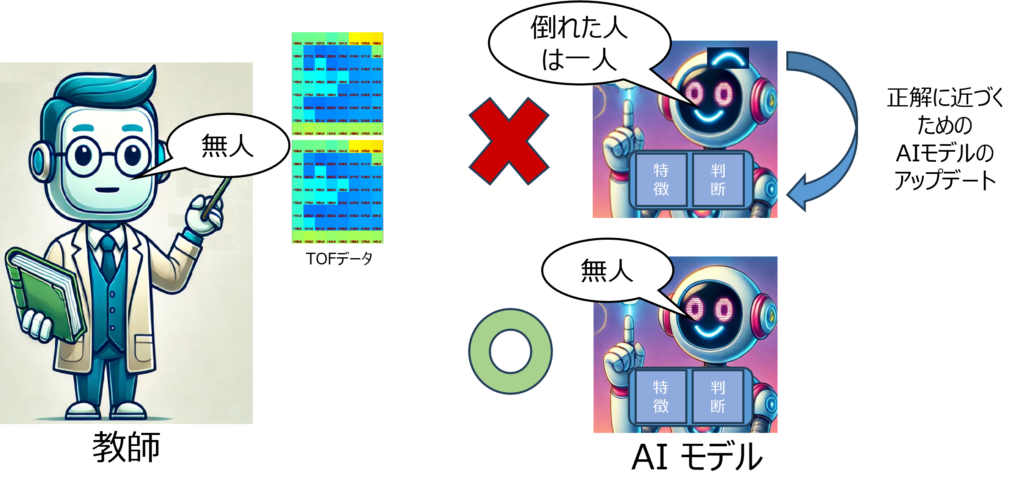
AIモデル評価とは?
学習用データと評価用データを分ける
データは2つの部分に分けられます。1つは学習用、もう1つは評価用です。
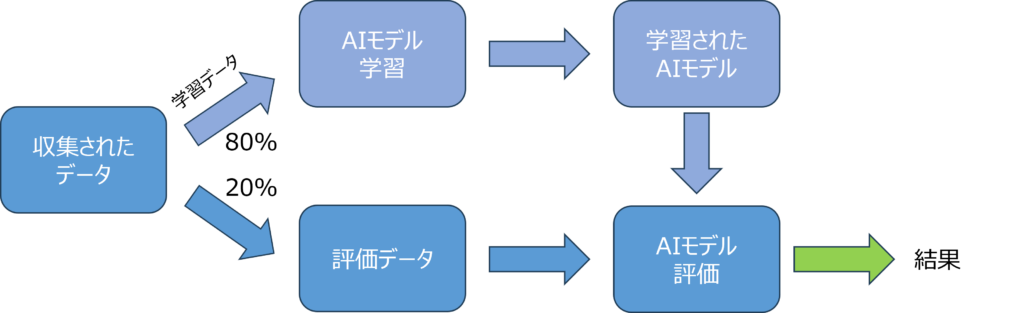
データは学習用と評価用に分けられます。学習用データセットは評価データとは独立させる必要があります。この独立性により、さまざまな環境でもAIが正確に状態を認識できるかをテストできます。
AIモデル評価
今回作成したAIモデルは、評価データに対して良好な性能を示しましたが、100%の精度には達していません。
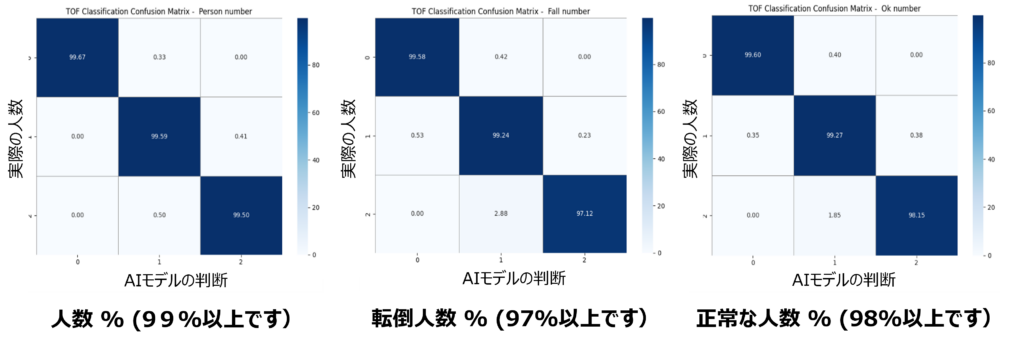
これは、転倒と立っている状態の間に明確な境界がない場合があるためです。また、このセンサーの課題として、人と大きな物体を区別できない点もあります。
PoC評価の実施
AIモデルも完成したので、実際の現場での対応能力をテストしました。実験の様子を撮影した動画もあるので、ぜひご覧ください。
実験のため、動画で私がいろいろな動きを試しています。また2人でトイレに入った想定で、AIモデル評価の実験した時の様子がわかる動画もアップしています。
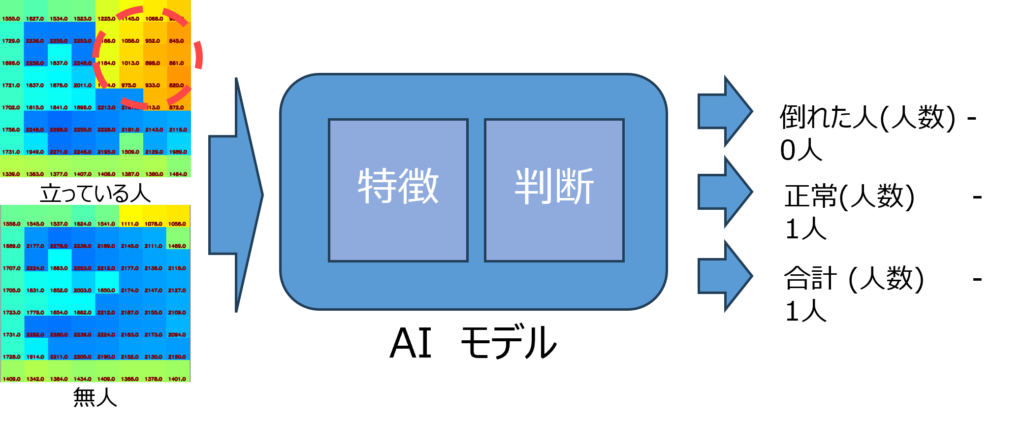
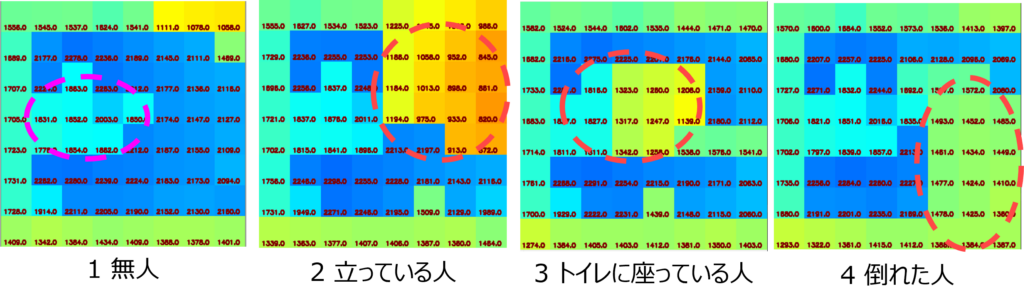
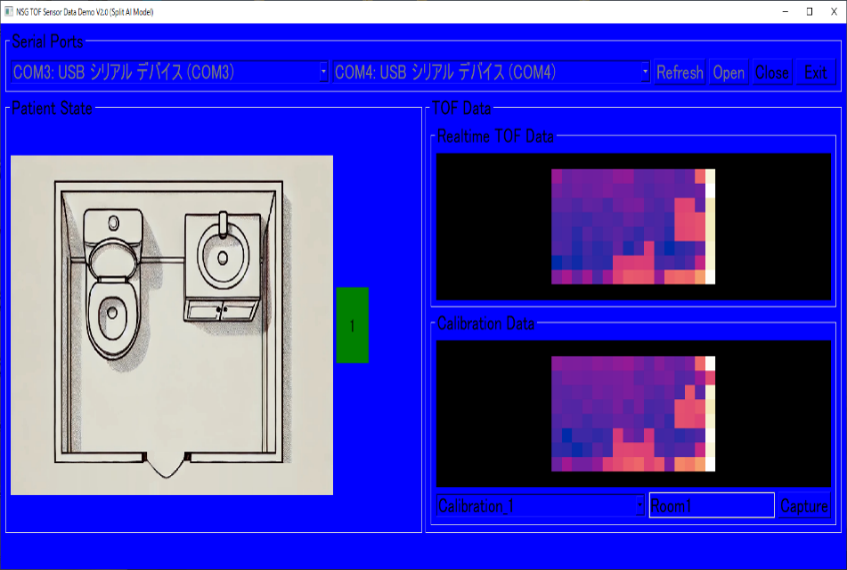
アプリでは、無人の場合は青、正常な状態は緑、異常な状態は赤で表示しました。
トイレでの人の動きに連動してアプリ画面の色が変わります。無人、1人立っている、2人立っている、などの状態をAIがそれぞれしっかりと検出しました。
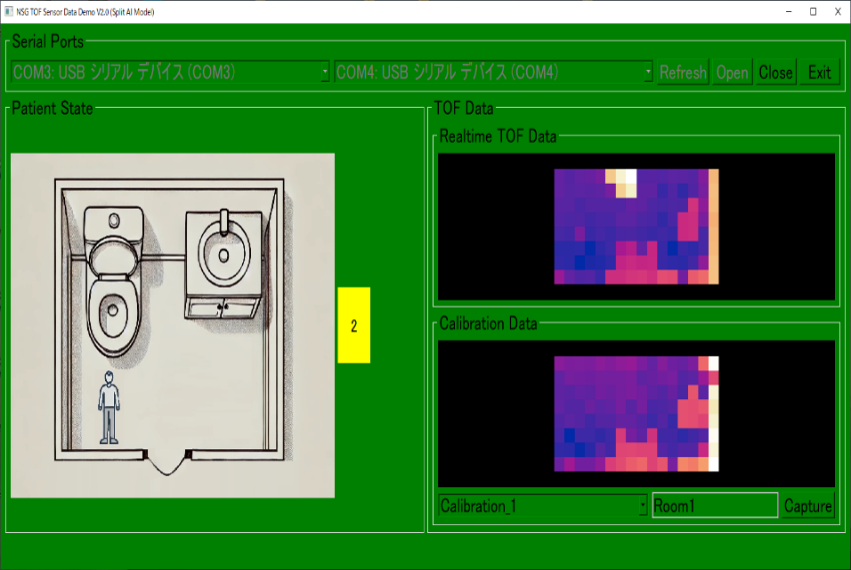
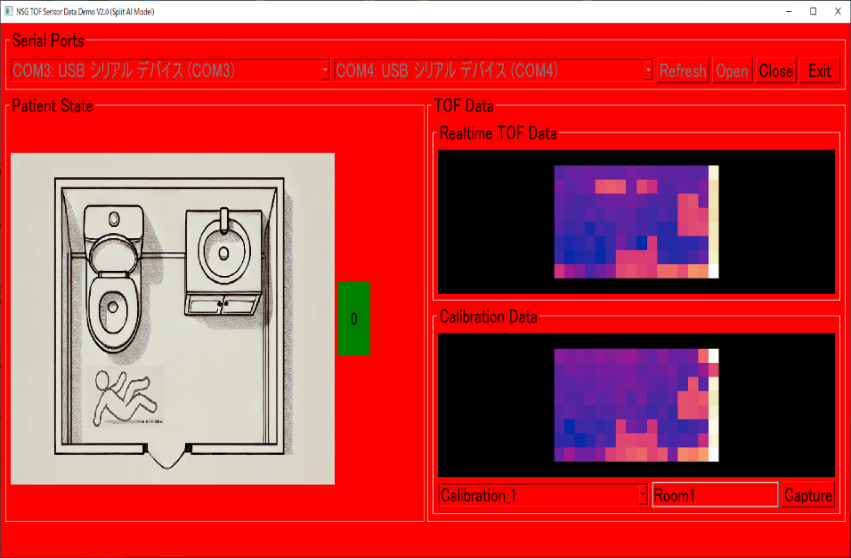
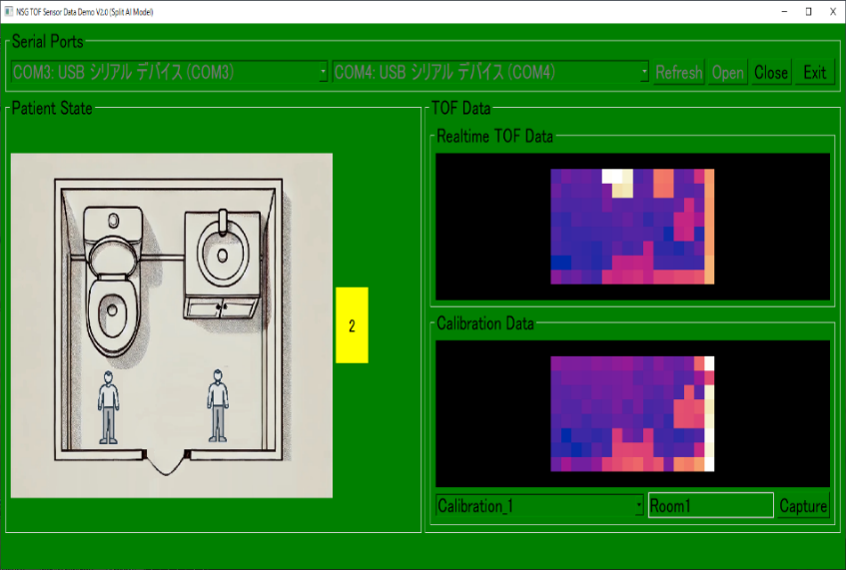
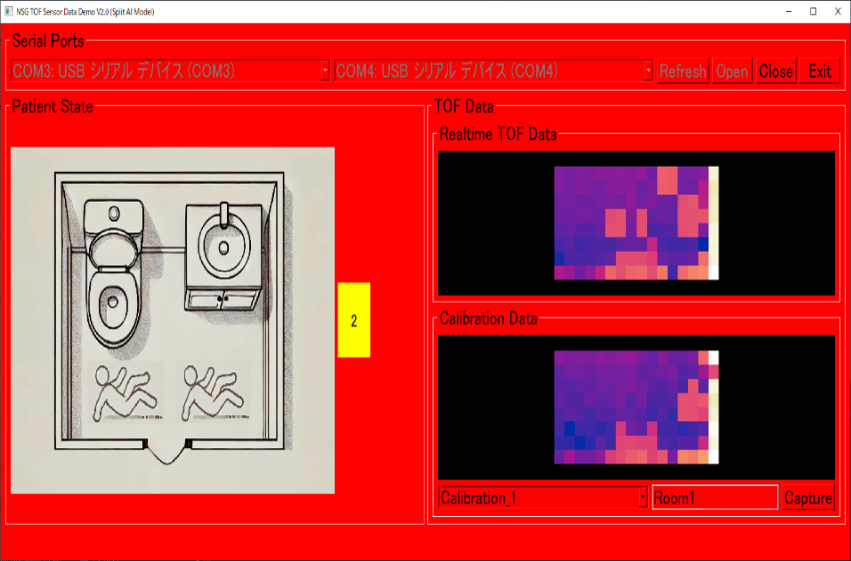
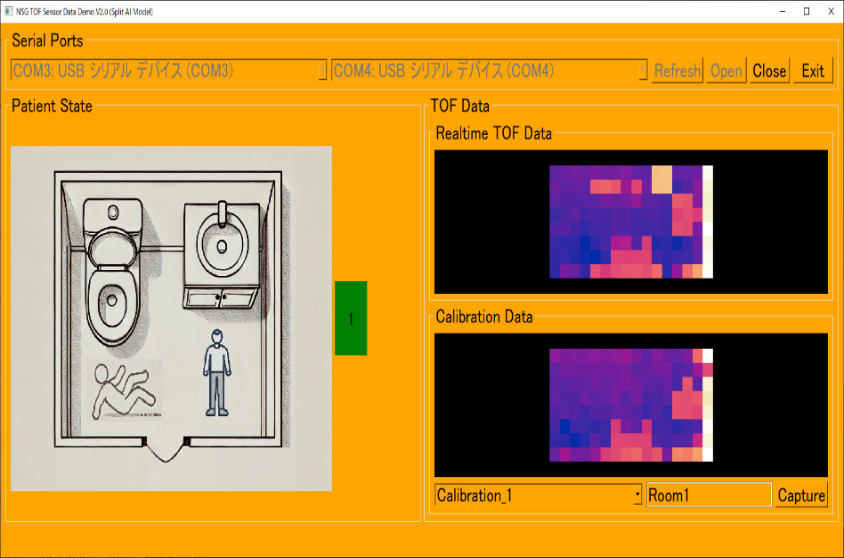
さらに、2人で居るときには、うち1人が立っていて1人が転倒している場合は黄色(注意)で示しました。これは、もし看護師と患者が2人同時に居る場合、看護師がサポートできるので即レッド(危険)ではない状態もあると考えたためです。実際のケースではAIだけの判断ではなく、看護師の携帯電話に電話するなど別のサポート手段を取る方法も考えられます。
AIモデル評価では2つの問題を指摘しましたが、実際のPoCにおけるAIの判定結果は有望でした。私の作ったAIモデルはトイレ部屋のレイアウト(建具の配置など)の違いにも対応できていました。
つまり、PoCは成功です!
いかがでしたか? さあ、次回のブログでは以下の内容について議論します。
- システムの改善点
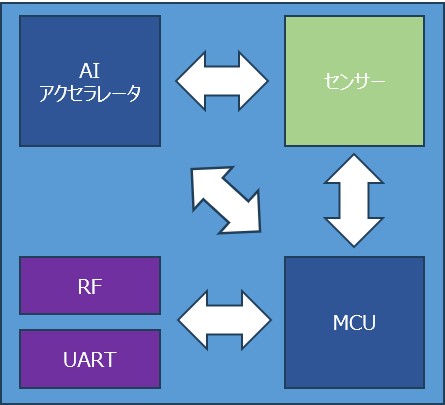
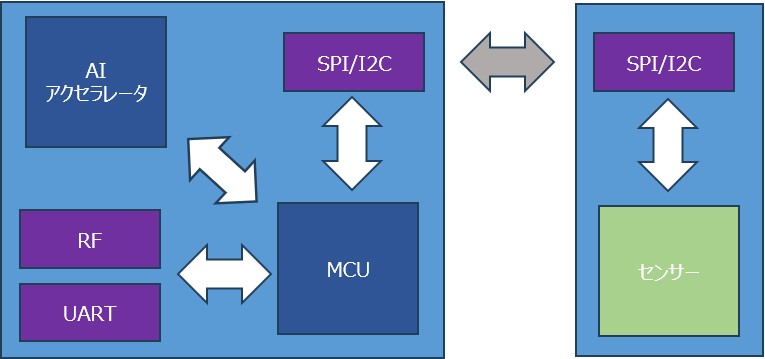
- システムのIoT MCUへの移植
- その他…
このPoCを実用的な商用製品へと発展させることを目指します。お楽しみに。