こんにちは。
前回までのブログでは、
・音や光など、どんな物理現象の「波」も、周波数の異なる”信号”の組み合わせでできていること。
・高校数学で学んだ三角関数と内積で「波」がどんな信号で構成されているのか検出できること。
これがフーリエ解析の前提であることをお伝えしました。
ある「波」から特定の信号を検出することを、”周波数成分を求める”とも言います。今日は、三角関数（正弦波）との内積を用いれば、「波」の周波数成分をもとめることができることをお示しします。
1Hzの周波数成分を求める
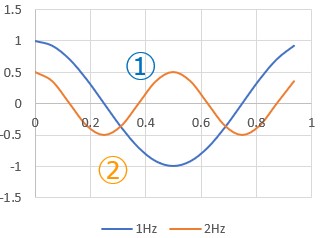
手始めに、図１のような入力信号①周波数１Hzで振幅1 入力信号②2Hzで振幅0.5 の特性の異なる２つの信号波を用意しました。※ 理解しやすくするために単純な振幅の信号にしています。
次に、計算のために1秒間で８つのタイミングを取り、図2に一覧表にしました。
また、これらの信号が検出ができているかを調べる正弦波として③1Hzのcosを用意しました。
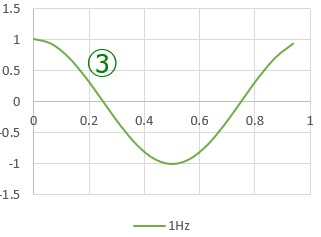
入力信号①とcos③、入力信号①とcos③が相関関係にあるかどうかは、内積を求めることで検出できます。
内積の式のおさらい
ここで、前回お伝えした内積の式を思い出してください。
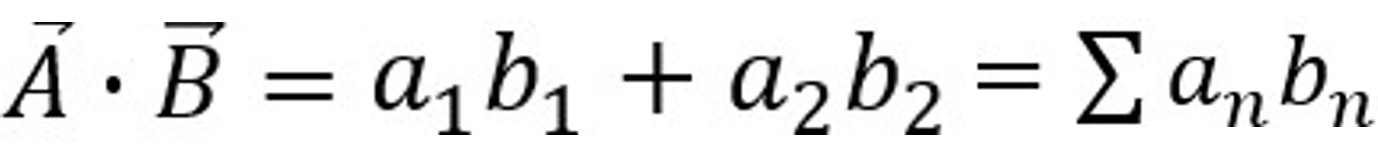
「nを時間とみなせば、信号処理的に内積は信号Aと信号Bの相関を求めていることと同じになります。」とお伝えしました。これを今回のお題に当てはめますと、入力信号①とcos③の各時間の積の和、 入力信号②とcos③の各時間の積の和が、 それぞれの内積①✖③、②✖③を求めていることと同じになりますね。
では①✖③から実際にやってみましょう。
時間0秒 ： 1 ✖ 1 = 1 0.125秒： 1/√2✖1/√2 =1/2 0.25秒：0✖0=0 … こんな感じです。
計算結果をさっきの一覧表に追加してみますとこんな感じになります。
右端赤枠に①✖③、②✖③の積の和の合計（横に足していきます）で求められる内積を示しました。
結果は、①周波数1Hzの入力信号と③との内積が4、②周波数2Hzの入力信号と③との内積が0でした。つまり⓵と③では相関があるので信号を検出できましたが、②と③は合計0なので相関が無いため、信号は検出されませんでした。
③cos1Hz用いて①の周波数1Hzの成分だけをうまく検出できましたね！
次に2Hzの正弦波(cos)を使い、同じように成分を求めてみます。
2Hzの周波数成分を求める
次に正弦波の周波数を少しずらして、入力信号①、②の周波数成分を求めてみます。
ずらした正弦波を④cos2Hzとして、用意しました。
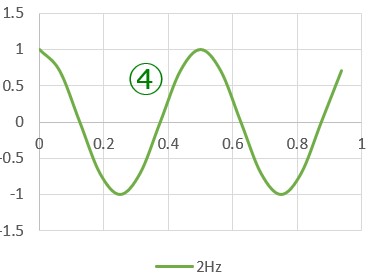
1Hzの時と同じように、入力信号①との内積①✖④、入力信号②との内積②✖④の和を求めてみると、図6のようになりました。
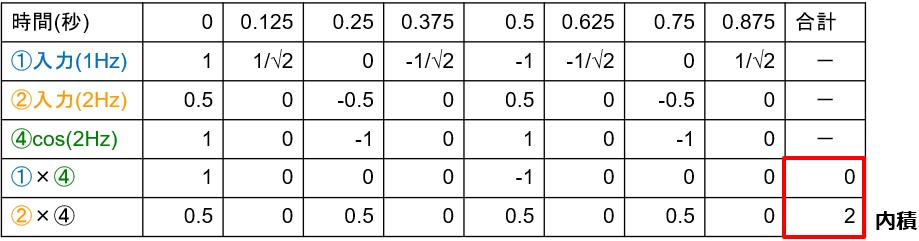
結果は、①周波数1Hzの信号に対しては内積が0、②周波数2Hzの信号に対しては内積が2です。
④を用いて、今度は②周波数2Hzの成分だけをうまく検出することができました！さらにこの値2は信号②の振幅に比例もしています。
周波数をずらすことの意味
これらの結果から、周波数を少しずつずらして正弦波との内積を求めれば、あらゆる周波数成分の大きさを検出できそうだな、と感じられると思います。
果たして本当に検出できるのか、次回はそれを検証してみましょう。
