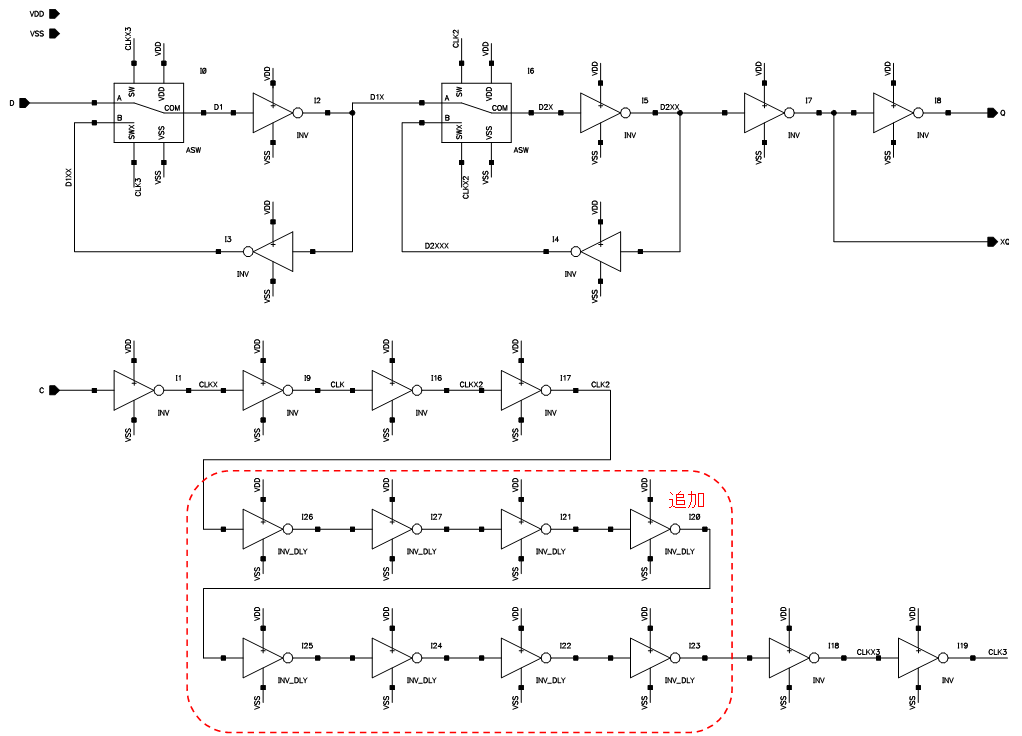
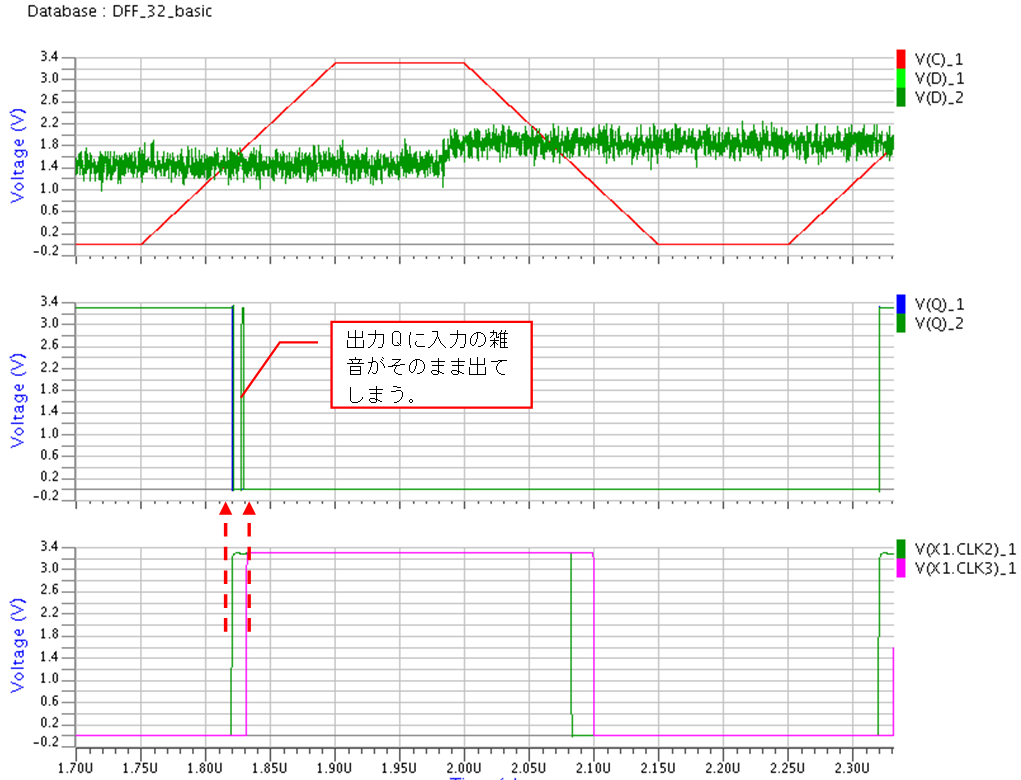
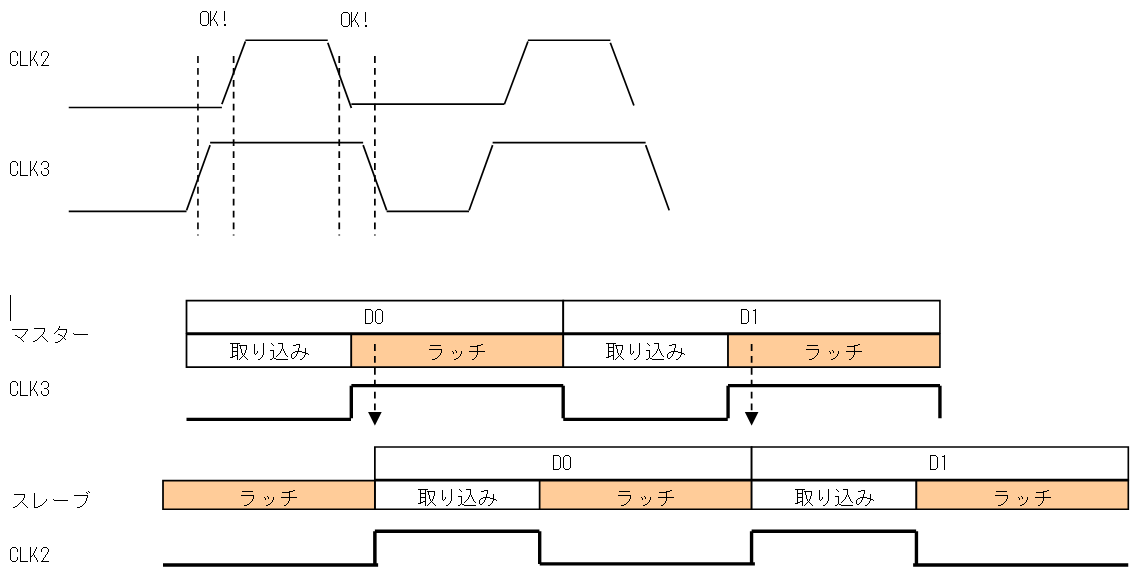
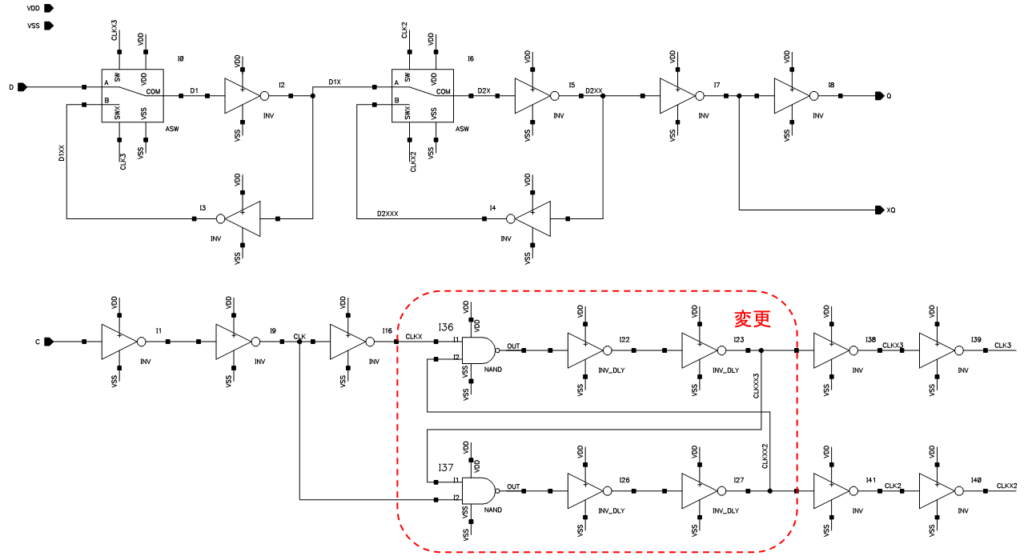
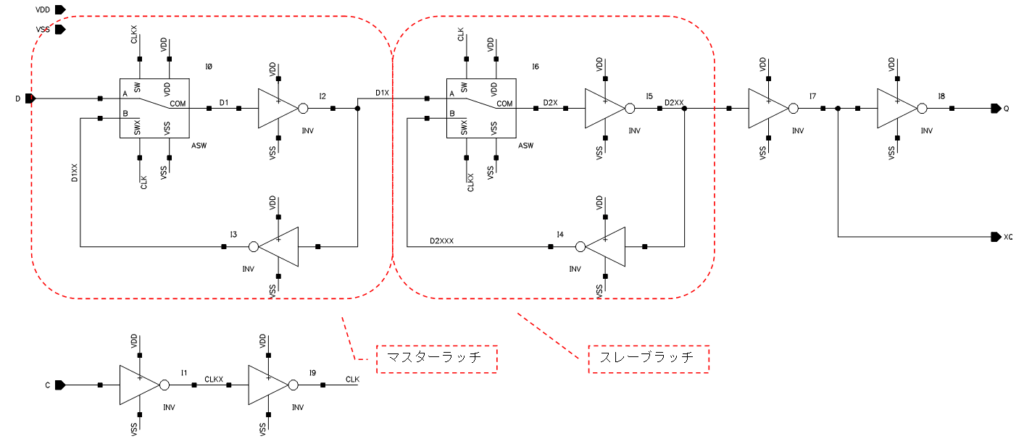
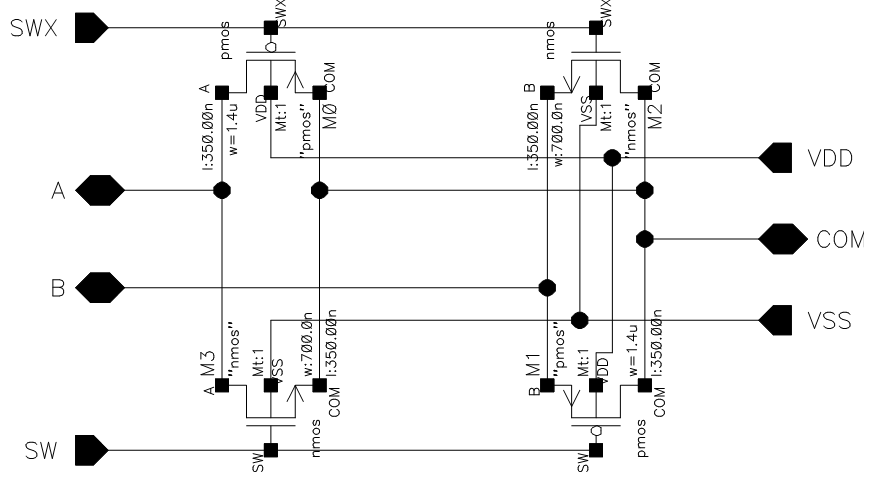
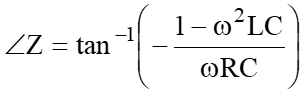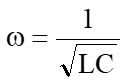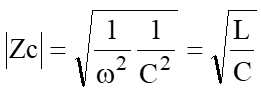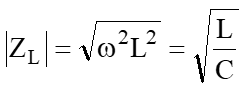今回は“誤り率”について少し触れてみたいと思います。
誤り率とは、その字のごとく符号を誤る確立です。つまり、エラーが発生することなので本当は電子機器ではあってはならないことですが、実際の電子回路の世界では、エラーとの戦いが見えない所で、いつも、そしてずっと続いているのです。エラーしないようにするにはどうすればいいのかを考えるのが、電子回路の設計者の仕事の始まりであり、ゴールでもあると思います。
エラーしないようにするには、なぜエラーしてしまうかを知る必要があります。
ではなぜエラーするかというと・・・それは雑音があるからです。
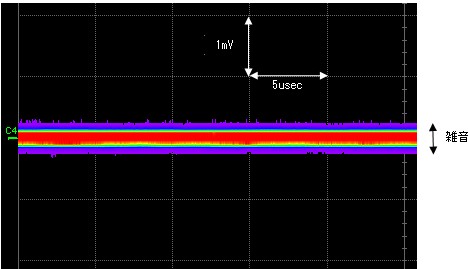
雑音はオシロスコープで何も信号を入れない状態でも観測できます。
最近のサンプリングオシロスコープは、サンプリングした結果に色をつけて表現してくれる機能があります。上の図の例だと真ん中の赤い部分は、サンプリングした結果、この電圧の確率が多いことを示していて、そこから離れていくと段々確率が減って色が変わってきています。中心から0.2mVもずれた電圧になることはほとんどないし、中心から1mVずれた電圧は一つもなかったと言っています。
例えば、信号が「今、1Vです」といっても、そこには必ず雑音が重畳されていて、あるときは1.01Vになってみたり、次に見たときは0.99Vになったりしているのが現実で、何千億の測定の中には0.5V以下になってエラーとなることがあるかも知れません。
どのくらいの確率でエラーするかを知り、エラーしても致命的な問題になる前にそれをいかに防ぐが勝負なのです。
雑音がなぜ発生するかについては、これを専門で研究している先生方に任せるとして、とにかく絶対零度(-273℃)にでもならない限り熱雑音(白色雑音とも言います)が必ず発生します(熱雑音以外にも、ショット雑音やフリッカー雑音などが発生します)。
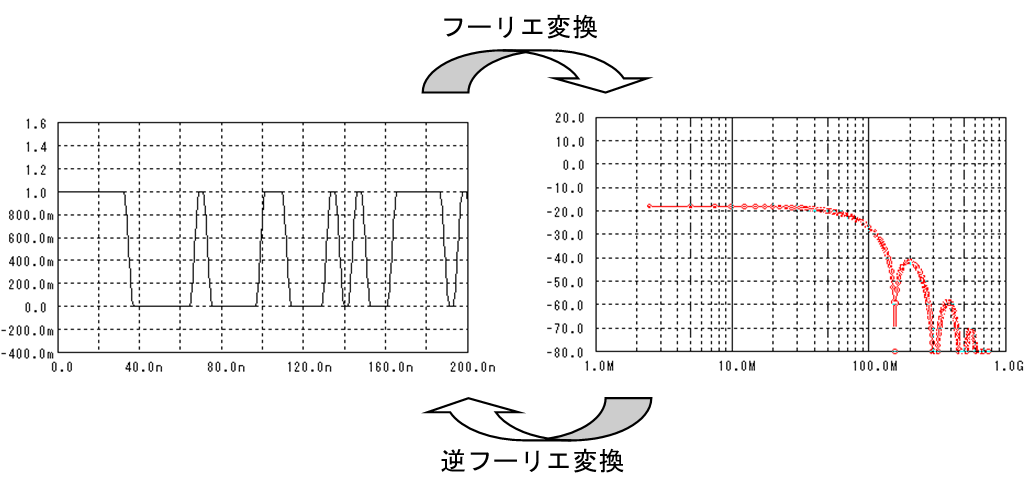
しかし、雑音の発生度合いは計算で予測することが可能です。その計算式を使ってどの様に雑音が発生するかをグラフにしたものを“正規分布”(ガウス分布とも)言います。
このグラフは中心が一番高くて、中心から離れるほど小さくなる曲線です。
雑音の発生確率は小さい振幅の雑音は頻繁に発生するけど、大きい振幅の雑音はめったに発生しないと言っています。
つまり、1.0Vに10mVの雑音が発生して1.01Vになる確率より、100mVの雑音が発生して1.1Vになる確立のほうが低いということです。当たり前のことなのですが、ここで大事なのは、それが計算で求めることができるということです。
例えば、10回測定して1回だけ1.01Vになったことが分かれば、1.1Vになるのは1万回に1回である事が計算で分かってしまうということです。
では具体的どんな計算をするかと言うと、次の様な計算をします。
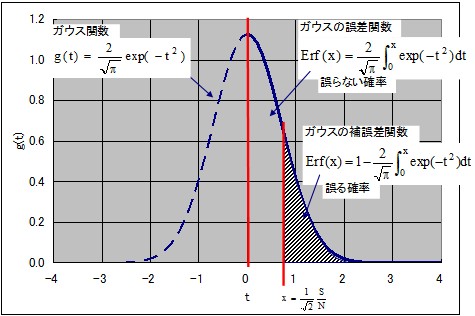
誤り率は、ガウス関数を積分して求めることが出来ます。中心からどこまでを積分するかはS/N(信号振幅と雑音の比)で決まっていて、積分する範囲が増えると(S/Nが良くなると)“誤らない確率”が増え、“誤る確率”が減ってきます。
つまり、どこまで積分するかを決めているS/Nが誤り率を決めていることになります。
S/Nって何かと言うと、信号電力/雑音電力で電力の比率です。
例えば、S/Nで20dBと言うことは電力比が100:1なので、電圧(電流)比は10:1になります。2乗がかかるかの違いがありますが、要は信号と雑音の比率です。
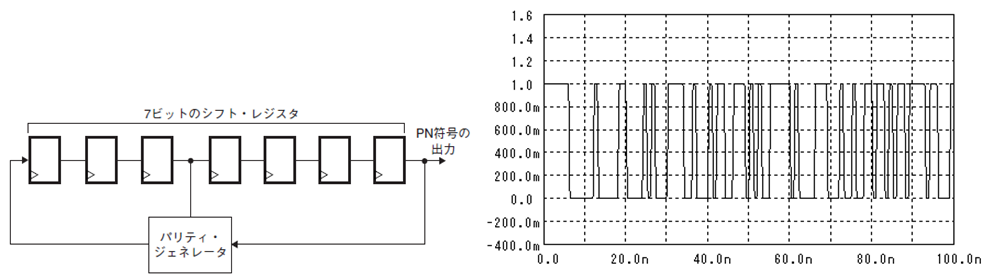
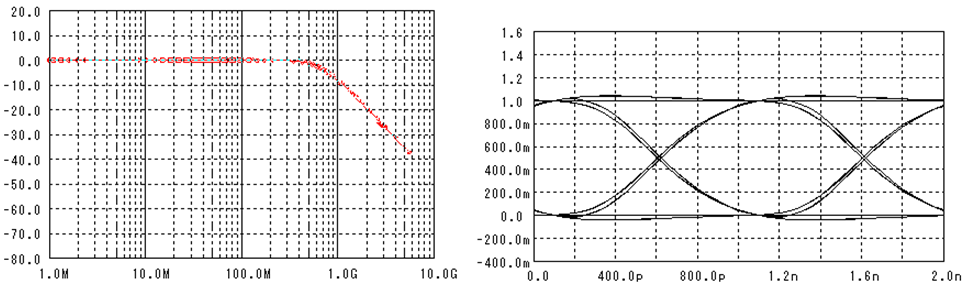
デジタル信号を“1”、“0”に識別する場合のS/Nと誤り率の関係を考えてみましょう。
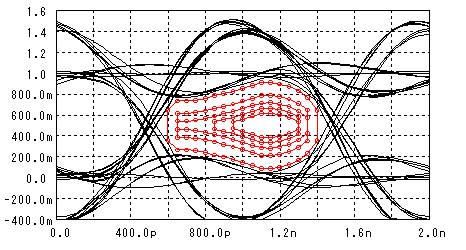
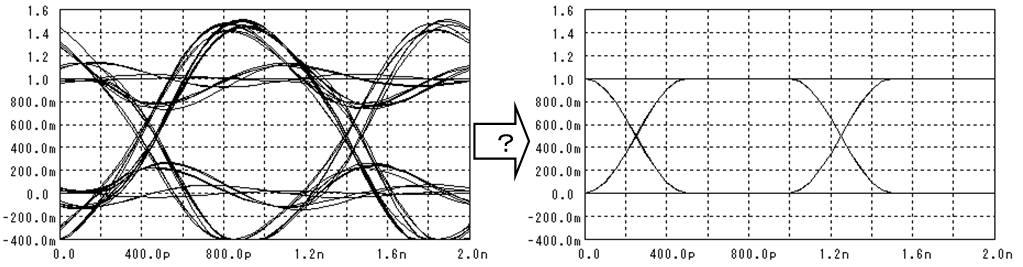
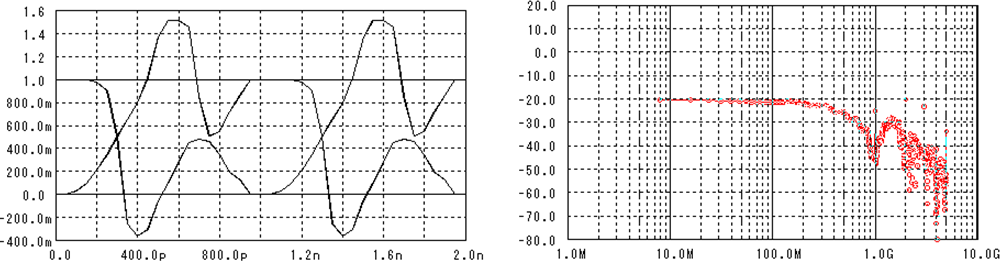
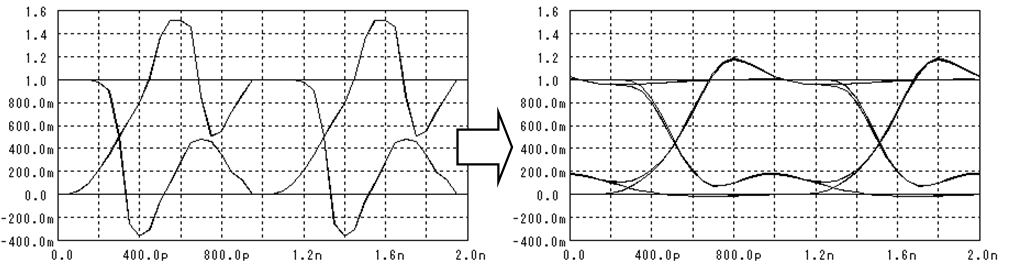
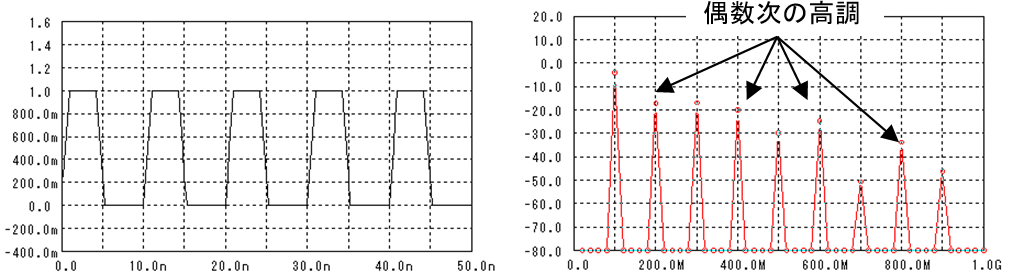
ランダムなデジタル信号を重ね書きすると下図の様になります。
この波形の事を“目”の様なので“アイパターン”と呼びます。
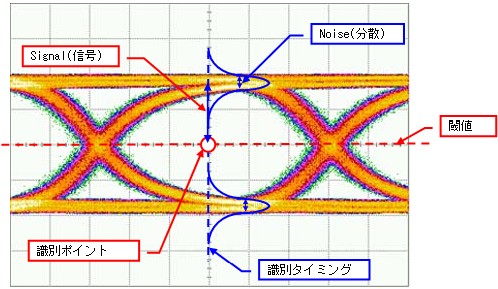
雑音がなければ“1”と“0”の電圧はいつも同じ値を示すのですが、雑音に依って電圧の値は“分散”します。この分散がS/NではNoiseに成ります。
上図の例では、“1”側と“0”側で同じ分散になっていますがショット雑音などが“1”のときだけ増える場合は(光通信など)、非対称になります。
一方、Signalは“1”“0”の各電圧と閾値までの差電圧になります。
例えば、閾値が“1”に近づくと、“1”側のSignalが小さくなり、”0”側のSignalが大きくなります。従って“1”=>“0”と誤る確率と、“0”=>“1”と誤る確率が閾値の位置に依って変わるので別々に計算をする必要があります。
雑音で電圧が少し分散しているので、閾値が“1”に近づくと“1”を“0”に誤る確率が高くなり、逆に閾値が“0”に近づくと“0”を“1”に誤る確率が高くなります。
デジタルデータを“1”、“0”と識別するタイミングに依っては波形のTr/Tfの影響を受けて閾値より十分離れる前に判別をしなくてはならなくなります。この場合も信号が小さくなったと計算できます。
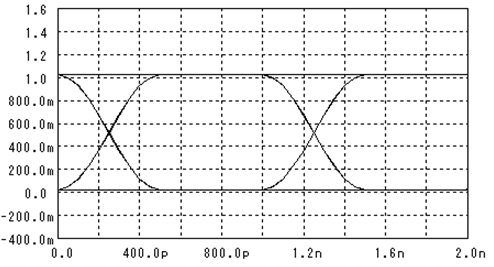
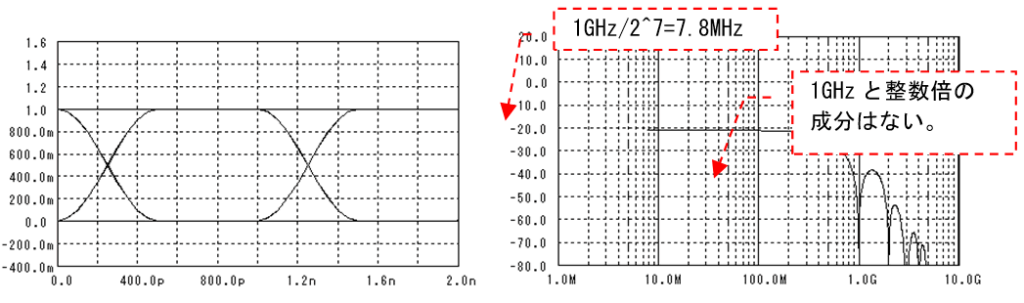
閾値と識別するタイミングで決まる“識別ポイント”を上下左右に変化させて、同じ誤り率の場所をつないだグラフを下図に載せました。円の内側に識別ポイントを調整すれば、その円の誤り率以下に成ることを意味します。
なお、この計算では“1”“0”共に分散=0.04としていて、閾値を0.5とした場合はS/N=20×Log(0.5/0.04)=22dBとなります。
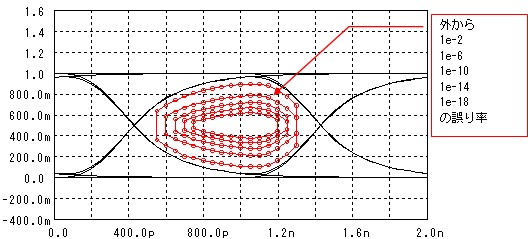
上図では、誤り率を1e-18以下(1Gbpsで20年に1.5回のエラー)にするためには、閾値は0.4~0.6の範囲に、識別タイミングは800ps~1200psの範囲に調整する必要がある事が分かります。干渉の少ない波形の場合は良いのですが、何らかの理由で波形の干渉が発生すると状況が変わります。
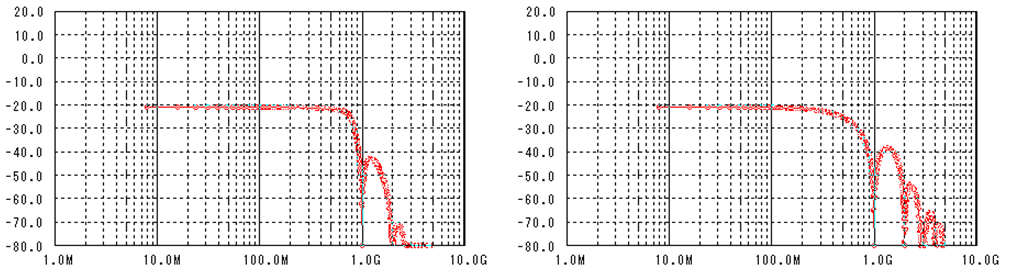
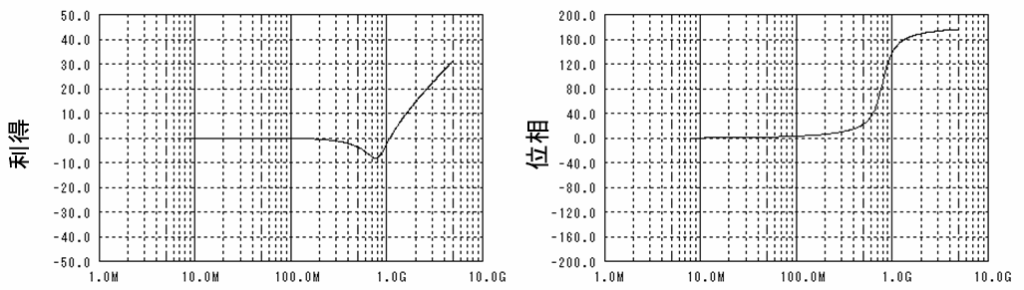
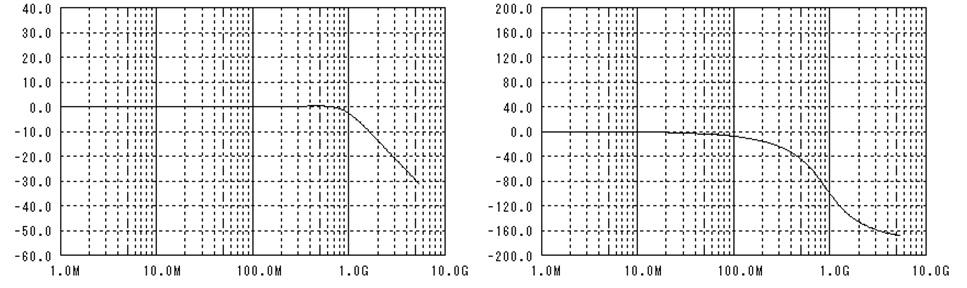
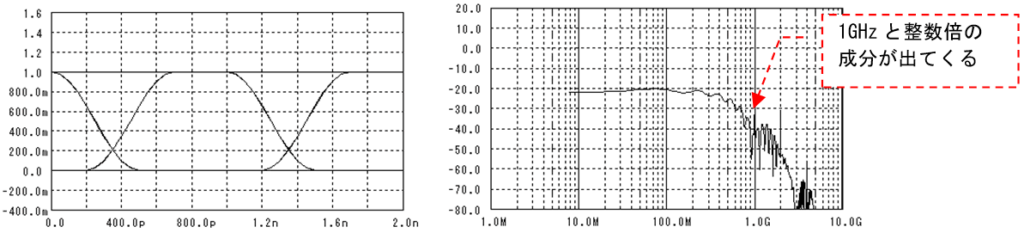
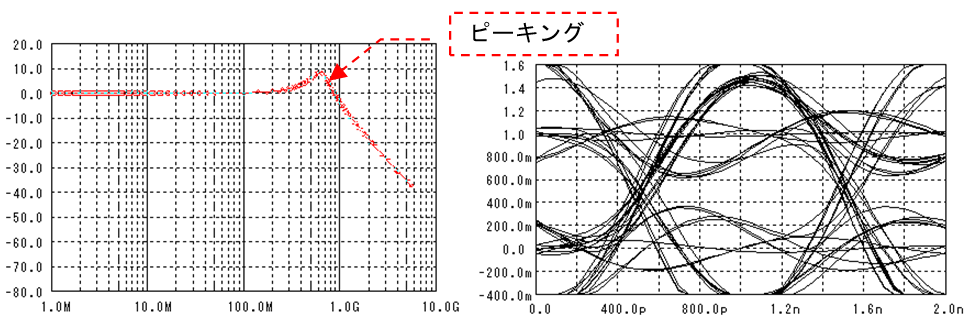
700MHzに5dB程度のピーキングがある2次LPFを通した場合の波形を上図に示します。
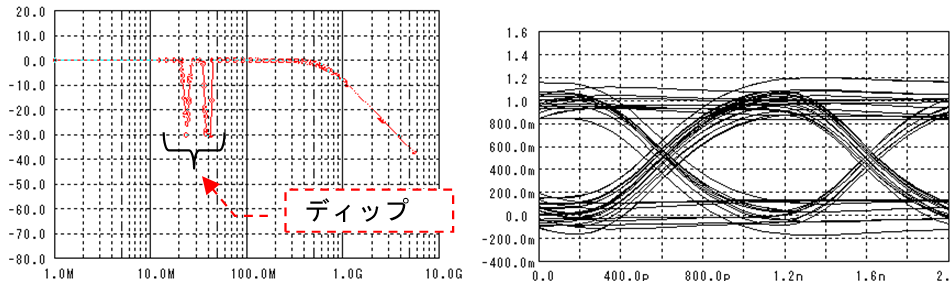
誤り率が1e-18以下となる閾値の範囲はあまり変化していませんが、識別タイミングの範囲は狭くなってしまいました。
信号の雑音と干渉でアイパターンはどんどん小さくなっていくので、低い誤り率を得るためには閾値や識別タイミングの制御を高精度にする必要があります。更には雑音や干渉は電源電圧/温度、素子バラツキなどで時々刻々変化するので、識別ポイントもその変化に追従する必要が出てきます。
例えば、別の識別機で上のような誤り率カーブを自分で計測して目標の範囲を求めてそこに識別ポイントを制御する・・・こうなると、もうアナログだけでは実現出来ないので、デジタルやファームの力が必要になり、すこし大掛かりな制御システムになってきます。
でも、弊社には強力なデジタル/ファームチームがいるので案外簡単に出来てしまう気がします(^^;
ランダム信号のアイパターンを見ていて、弓道の「的」を思い出しました。緊張やプレッシャーで的が小さく見えていた時は、心の700MHzに5dB程度のピーキングが発生していたのだと・・いま分かりました(汗)
さて、次はよろしければ「反射」について読んでみてください。
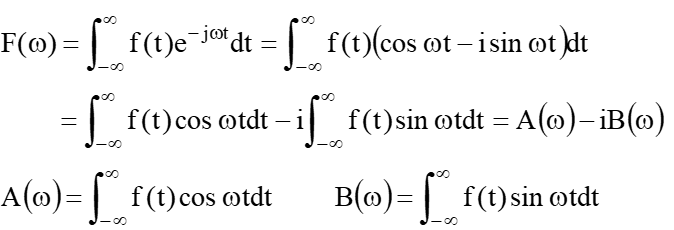
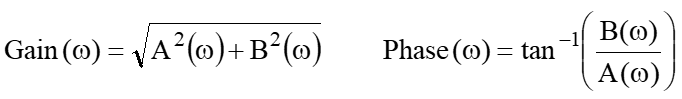


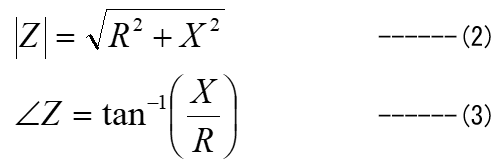
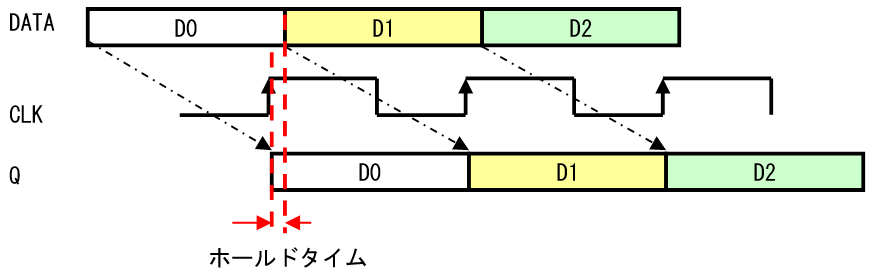
 は、
は、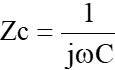
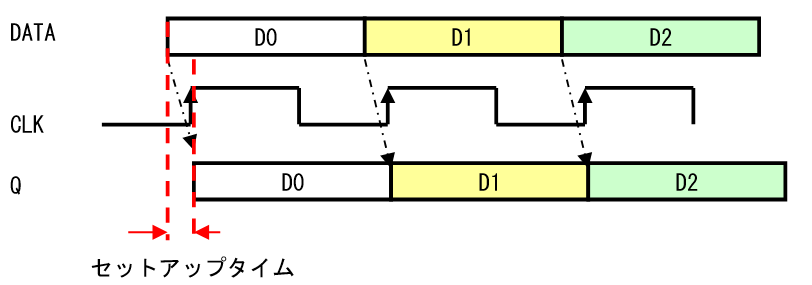
 は、
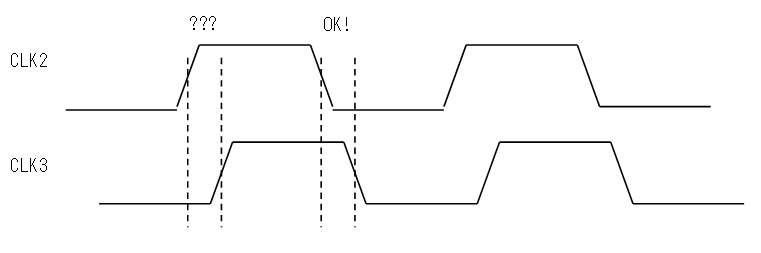
は、