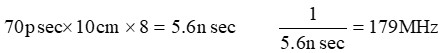反射を使って何かを調べると言うと・・・TDRという測定方法があるのをご存知ですか？
“TDR”をGoogleで検索すると・・・ホテルご予約の案内。東京ディズニーリゾート・・・の略でもあるのですが（汗） ここではTime Domain Reflectometry の略です。
TDRという測定法
直訳すれば「時間軸の反射測定」となります。今まで反射の波形を時間軸で説明してきたのに何をいまさらと思われるかも知れませんが、この測定はSパラメータと同じく反射を測定する方法のひとつで、反射がどこで発生しているか、その場所を突き止めることが出来ます。
昔の高価なオシロスコープにはTDR測定用の端子があって、ここに同軸ケーブルを経由して評価ボードを接続します。そうすると評価ボード（非測定物）のどの辺りで反射が起きていて、しかもそれが特性インピーダンスより大きいのか小さいのかもわかってしまうと言う優れものです。
評価ボードのコネクタ部分が悪いのか、LSIの入力が駄目なのか、ストリップラインの曲がっている場所で反射してるのか をオシロスコープの波形を見ればすぐに分かり、しかも、指で触るとリアルタイムに波形が変化したので、非常に直感的で、まさに体で感じることが出来る優れた測定方法です。まだ駆出し頃、反射しているポイント指で探って、そこに指と同じ回路を追加して反射の影響を出来るだけ減らすことと格闘していました。
ちなみな私の人差し指の等価回路は、10pFと5.1Ωの直列でした。
TDRのメリット
インピーダンスの整合を調整する方法にはスミスチャートを使う方法（別の機会に紹介したいと思います）があります。しかしこの方法はRF回路などインピーダンスを整合させる周波数範囲が狭い場合には非常に有効ですが、NRZ信号などの様に信号成分が広帯域におよんでいて、広い周波数範囲でインピーダンス整合をとる場合には有効とは言えません。
その点、TDRは非常に広い周波数範囲でインピーダンスの整合を調整するのに都合の良い測定方法です。
反射波を用いたTDRの測定原理とは
TDRの測定原理は非常に簡単です。非測定物（なぞのモジュール）に向かって非常に立ち上がり時間の短いパルスを送出し、その反射波を観測するだけです。
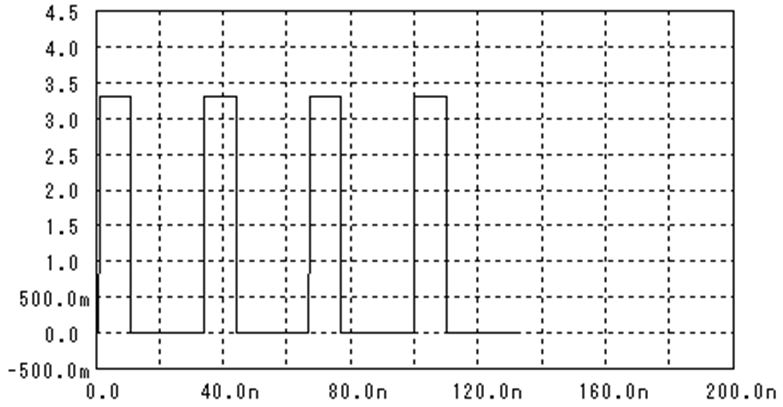
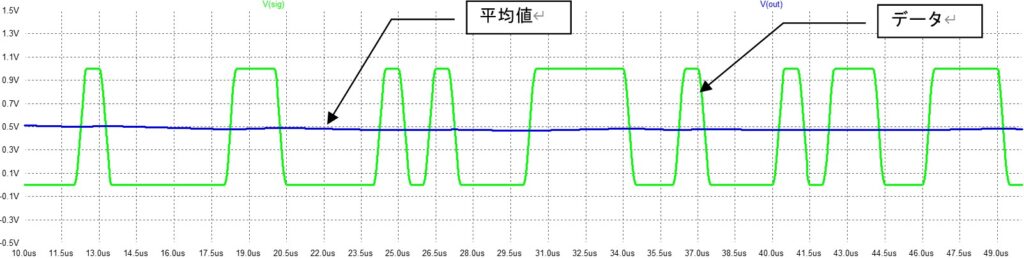
あるモジュールの端子に同軸ケーブルを接続してTDRを測定した結果、次の様な波形が出てきたとします。
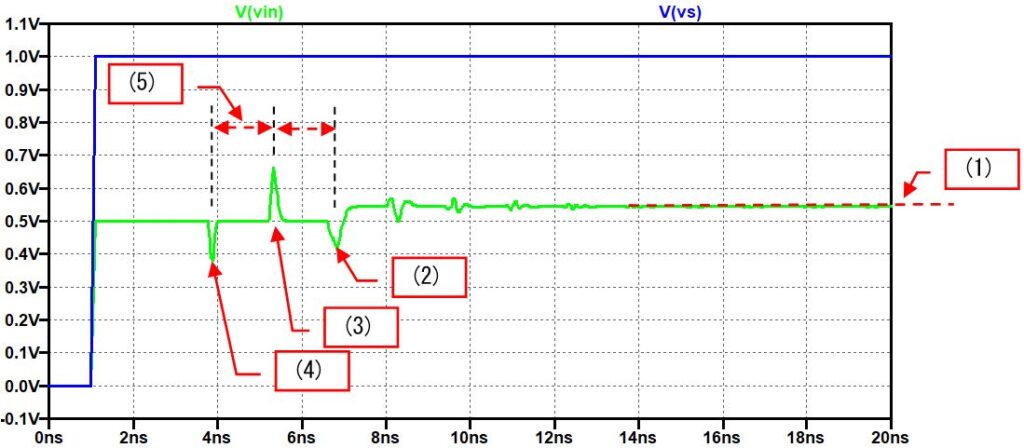
つまり、V(vs)：青の信号を送信した結果、信号源のインピーダンス整合をする抵抗RsにV(vin)：緑の波形が現れたとします。実はこの波形から色んなことがわかるのです。
TDR測定で分かること
- 波形の落ち着いた場所が中心(0.5V)から少し上にずれている。
これは、終端抵抗が信号源インピーダンスから少し大きめになっていることを意味します。長い時間その値を保っていられるのは直流に近い成分であることを意味しているので、直流結合で接続されている終端抵抗が50Ωより10%ほど大きめになっていることが分かります。LSI内に終端抵抗を実装した場合は有りうることです。 - 終端される前に一旦、電圧が低くなっています。短い時間だけ、つまり高周波でインピーダンスが低くなると言うことは・・・信号線とGNDの間にコンデンサが入っていることを意味します。つまり、終端抵抗と並列にコンデンサが付いていることが分かります。
- 少し手前に来ると、インピーダンスが高くなっている部分があります。短い時間だけ、つまり、高周波だけインピーダンスが高くなると言うことは・・・信号に直列にインダクタが入っている事に成ります。原因はモジュールを空けないと分かりませんが、信号の接続VIAかもしれません。
- 更に手前に戻って来ると、再びインピーダンスが低くなっている場所があります。ここにも信号とGND間にコンデンサが入っていることが分かります。この部分はモジュールの入り口なので、コネクタと接続するためにボードのパターンが太くなっているのかもしれません。
- インピーダンスがずれている間の時間がおよそ1.4nsecで、2箇所が同じ位の間隔になっていることが分かります。もし、モジュール内のボードがFR-4（ガラスエポキシ基板の代表的な例）で作られているとすれば、伝播遅延時間は70psec/cmなので、1.4nsecは20cmで作られる事に成ります。反射波は行って帰ってきていますので、ボード上では約10cmの距離に換算できます。
ブラックボックスを開封せずに波形で推定する
TDR測定の結果と答え合わせ
なぞのモジュールを開けた結果は次の通りです。
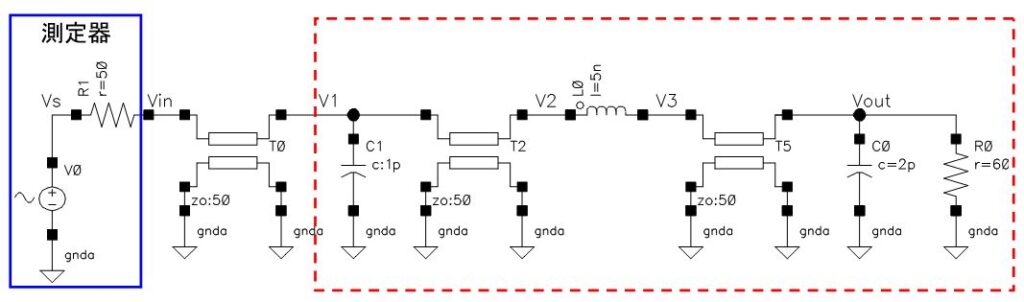
ほぼ、波形から推定した結果を同じ回路となっていることが分かります。
なおTDRの更に詳しくは、下記を参照してください。
https://literature.cdn.keysight.com/litweb/pdf/5989-4149JAJP.pdf
TDR測定は、中を触ることの出来ない回路（例えば、モジュールやLSIなど）のインピーダンス整合がどこでずれているかを外部から知ることが出来るので、非常に重宝な測定方法です。
超音波も反射波を用いた測定法の１種
反射波を使った方法は他にもあり、超音波を発射して、反射波を解析することで反射を起こした物体の状態(硬さなど)や距離を求めて映像にする超音波診断装置は、良い代表例だと思います。
超音波
https://ja.wikipedia.org/wiki/%E8%B6%85%E9%9F%B3%E6%B3%A2%E6%A4%9C%E6%9F%BB
ここまで書いて、イルカは超音波診断装置を何万年も前から使っていたのだと、気が付きました（汗）
光を捉えると言う点では人も目も優れていて、ろうそくの光でも夏の海岸でも本が読めます。
しかし、自然に入ってくる光（情報）を見るだけではなく、自ら音波(言葉や行動)を発して、その反射(対話)を感じることで、目では見えない相手の内側や本質や大切なものが見えてくるのだ と教えられた気がしています。
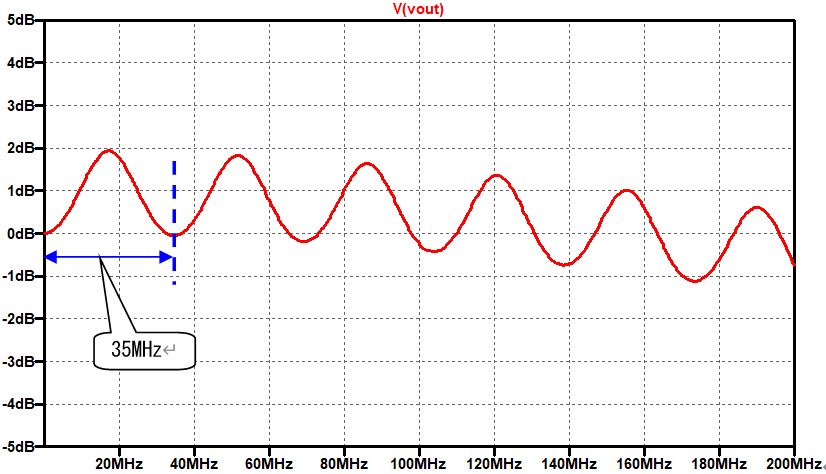
です。
の信号ならちょうど一周期分がぴったり伝送路に入ります。
周期では35.7MHzと成り、
周期では17.9MHzと成ります。
波長になる周波数からかな”と、答えていました。
波長になる周波数から。場合に依っては
波長から”と答えないといけなかった事が分かってしまいました（大汗）
