今回は、歪んだ波形を元のきれいな波形に戻すにはどんなフィルタが必要か?について紹介したいと思います。
前回の記事はこちら
実験や評価などでオシロスコープを使ったことがあると思います。その時に例えば下図(左)のような波形が観測されたとします。この波形を下図(右)の様にきれいな波形に戻すためには、どんなフィルタを通せば良いのでしょうか?
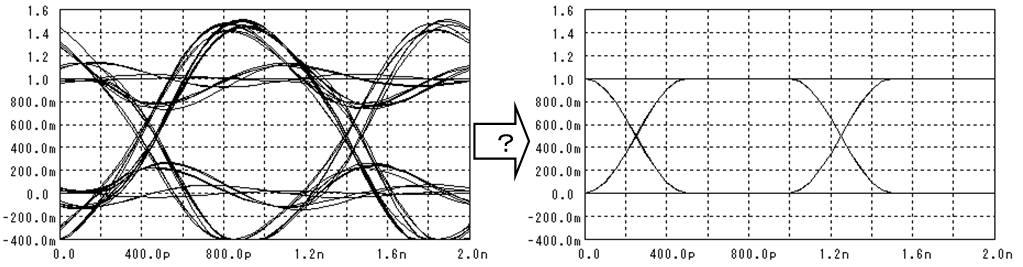
左の波形はオーバーシュートが発生しているので、その分は減らさないといけないので何らかのLPFが必要なのは分かります。しかし、単なるLPFではTr/Tfが大きくなり(波形がなまり)、元の波形に戻りそうにありません。
どういうフィルタを使えば、きれいになるかを求めるにはフーリエ変換が活用できます。
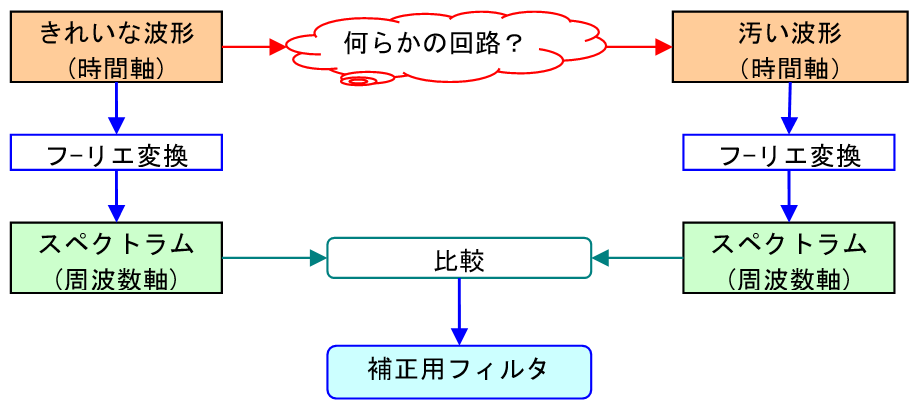
時間軸の波形データを周波数軸に変換(フーリエ変換)すれば、その波形の周波数成分が分かります。何らかの回路で乱れてしまった波形と、その前のきれいな波形の周波数成分(スペクトラム)を比較すれば、必要な補正フィルタを計算で求めることが出来ます。
図 3 汚い波形のスペクトラム(左)ときれいな波形のスペクトラム(右)
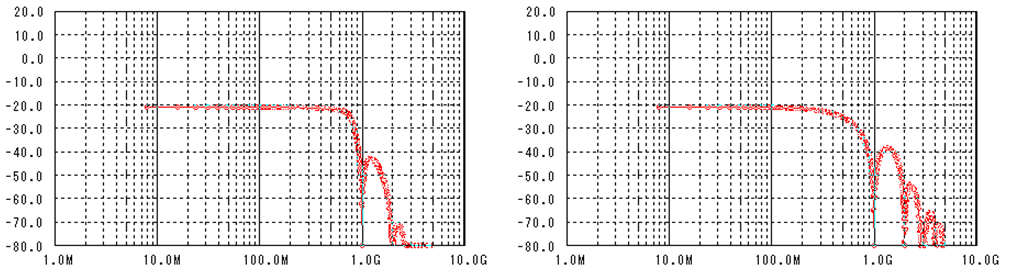
図 4 波形を補正するのに必要なフィルタ
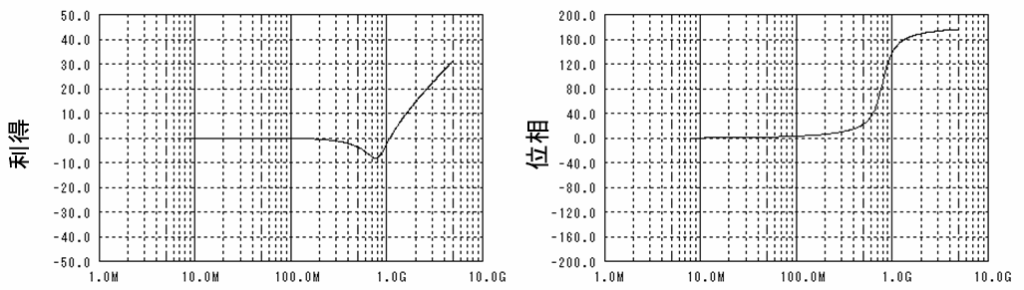
周波数成分(スペクトラム)には位相情報も有りますので、これも利得と同じように引き算することで、目標のフィルタ特性が位相特性も含めて計算できます。
上の例では、800MHz辺りの利得を減らして、それより高い周波数はそのまま利得を高くしていくフィルタを使えば元に戻ることが分かります。
補正フィルタの形がピーキングを持たせたLPFの逆特性になっていることに気が付いたでしょうか? そうです、オーバーシュートがある汚い波形は、800MHzにピーキングを持たせたLPFを使って作りました。
なんとなく定型フィルタを使って波形を歪ませた所が、少しインチキ臭いような気がしてしまう方のために、次のような勝手に入力した波形で同じ事をしてみたいと思います。
図 5 任意の歪んだ波形とそのスペクトラム
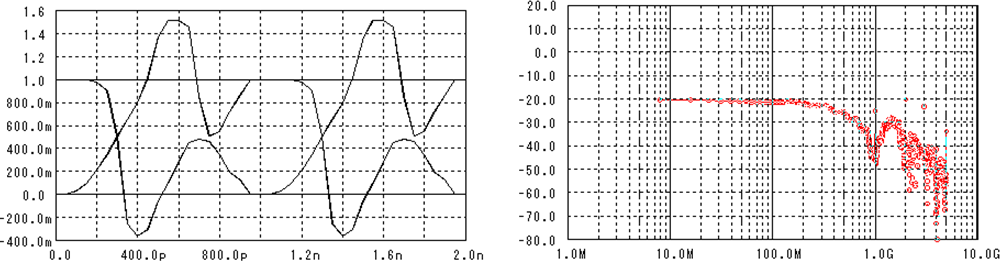
立ち上がりと立下りに大きなオーバーシュートを意図的に作った波形です。このままではまともに受信が出来ず、エラーが発生してしまいます。これをきれいな波形戻すために必要なフィルタを計算で求めてみましょう。
図 6 歪んだ波形をきれいな波形に戻すフィルタ特性
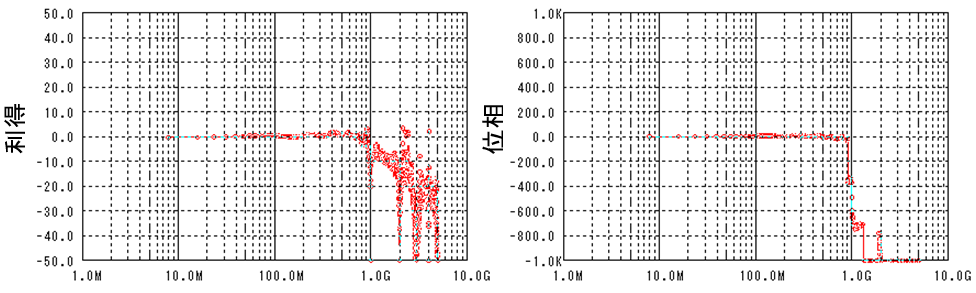
どんなフィルタなのか解読が難しいくらい複雑なフィルタになっていますが、利得特性は1GHz辺りにカットオフがあり、位相特性も1GHzで急峻に遅れていることが分かります。
このフィルタに上の汚い波形を入力すると、次の波形が出てきます。
図 7 元のきれいな波形に戻った状態
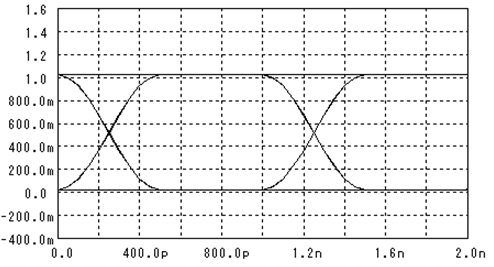
周波数成分を理想的な波形と比較して、その差分を補正フィルタで補正した周波数成分を逆フーリエ変換したのですから、当たり前の結果と言えばそうなのですが、きれいに目標通りの波形が出てくると、嬉しいものです。
実際には上のような複雑なフィルタは作れません。特性の近いフィルタで代替してみましょう。ゲイン特性を見るとカットオフ周波数がだいたい1GHz辺りのLPFで、ガタガタしているものの全体としては2次になっている様に見えます(10GHzでは-40dBを通過しそうです)・・・なので、次のLPFで代替してみます。
図 8 代替のフィルタ特性
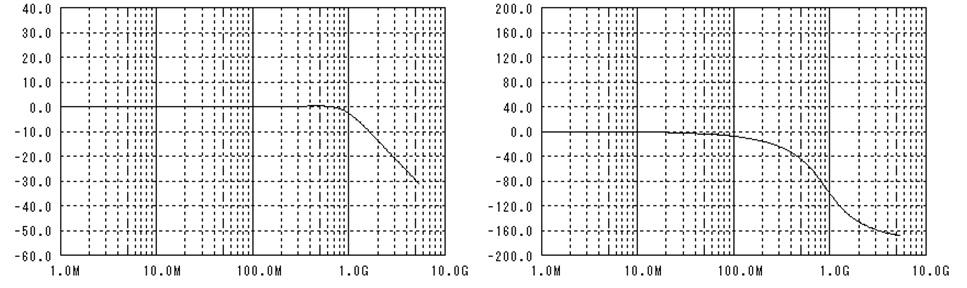
位相特性は計算結果の様に急速には変化できません。この部分はあきらめるとして、どんな結果になるか、任意の歪んだ波形を入力してみましょう。
図 9 代替フィルタの効果
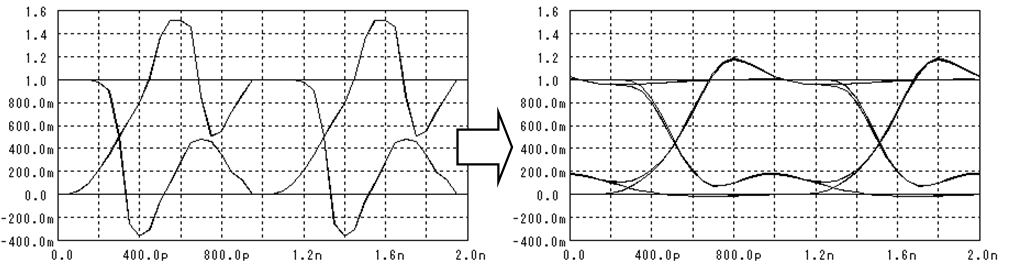
位相特性をあきらめたためと思いますが、完全にはきれいな波形にはなっていません。
しかし、この波形であればエラーをせずに受信が出来そうです。
フーリエ変換を使えば、測定器などから波形データの実際の測定結果を取り込んで、どのようなフィルタにすれば波形が補正できるかを(感ではなく)計算で求めることが出来ます。また、このようにして計算したフィルタは、実際に回路を作らなくてもその効果を計算で確かめることが出来るので、回路設計の前段階の検討にフーリエ変換は非常に効果的です。