アナログ回路設計をするうえで避けて通れない変換として、フーリエ変換があります。
フーリエ変換/逆フーリエ変換とは何か?
“フーリエ変換”とは、フランスの数学者であるフーリエが発見した定理のフーリエ積分を利用した、時間領域(波形)と周波数領域(波形)の変換公式です。
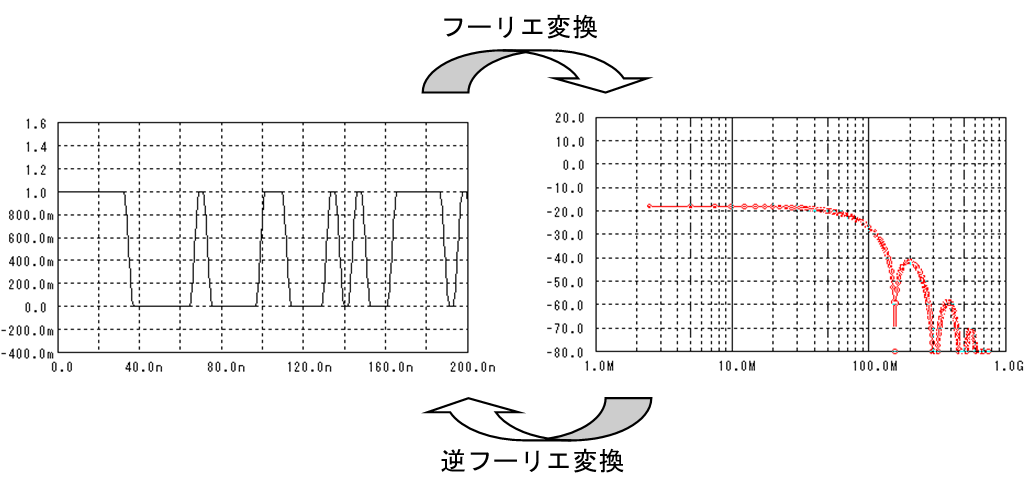
つまり、“フーリエ変換”は時間軸の波形を、周波数軸のグラフに変換することです。
逆に周波数軸のグラフを時間軸の波形に変換することを“逆フーリエ変換”と呼びます。
図 1
フーリエ変換の根底にある基本原理は、「全ての周期的な波形は、様々な周波数の正弦波の組み合わせで成り立っている」です。
要は、波形がどういう周波数と位相の正弦波に分解できるかを計算するのがフーリエ変換で、色んな周波数と位相の正弦波を足し合わせるとどんな波形になるかを計算するのが逆フーリエ変換です。
世の中の全ての出来事は、時間と共にその量が変化しているに過ぎないとすれば、この変換はアナログ設計をする上でだけではなく、世の中の現象を理解/分析するために非常に有効な変換だと思います。
フーリエ変換の公式
基本的な公式は色々な文献に載っていますが、次の公式が一般的と思います。
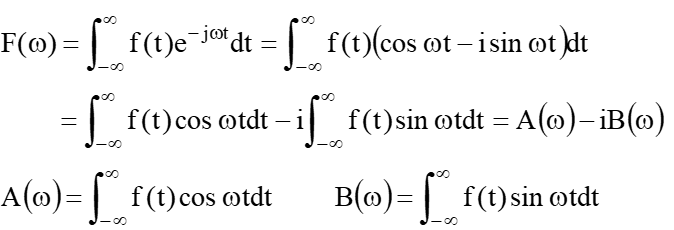
ここで、A(ω)とB(ω)は実部と虚部なので、振幅と位相成分は、
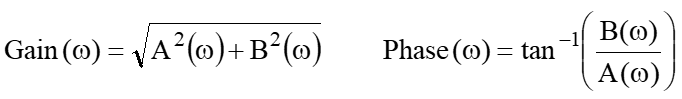
となります。例えば、ある波形に10KHzの実部がどの位入っているかは、波形f(t)とcos(2π10K t)を掛け算して、時間を-∞から+∞まで積分すれば良いって事になります。虚部はsin(2π10K t)を掛け算して同じように-∞から+∞まで積分すれば良いのです。
逆フーリエ変換の公式
それでは逆はどうなるかと言うと、似たような感じですが次のようになります。
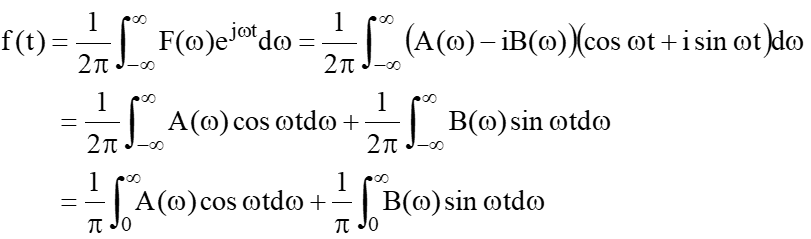
つまり、周波数特性を実部と虚部に分けて、実部にはcosωtを虚部にはsinωtを掛け算し、全周波数帯に対して積分する(たし合わせる)と元の波形に戻ることになります。
波形と周波数特性の特徴
この面倒な計算を電卓で行うことは非常に手間がかかるので、かなり昔になるのですが、変換が簡単に出来る“手作りアプリ”Visual Basic で作りました。
このアプリを使って、波形と周波数特性の特徴を説明したいと思います。
(A)正弦波
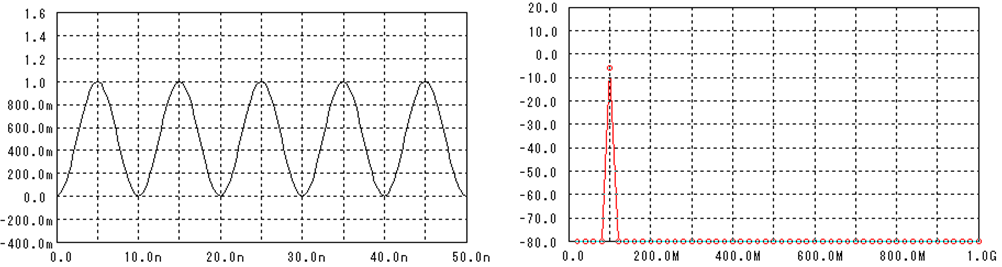
当たり前のことですが、100MHzの正弦波(左)を変換すると100MHzの周波数成分(右)しか出てきません。
(B)三角波
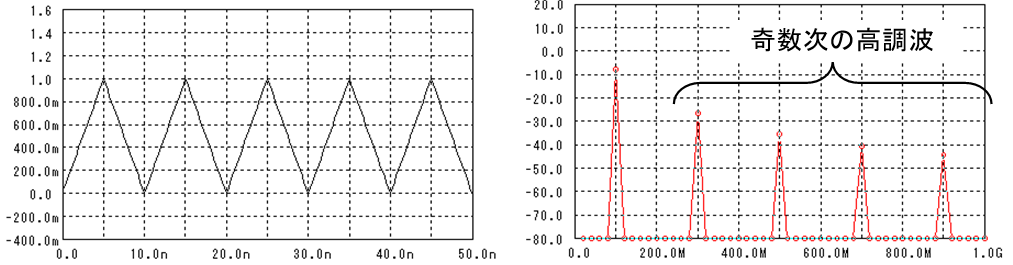
三角波にすると、奇数次の高調波が出てきます。
(C)矩形波
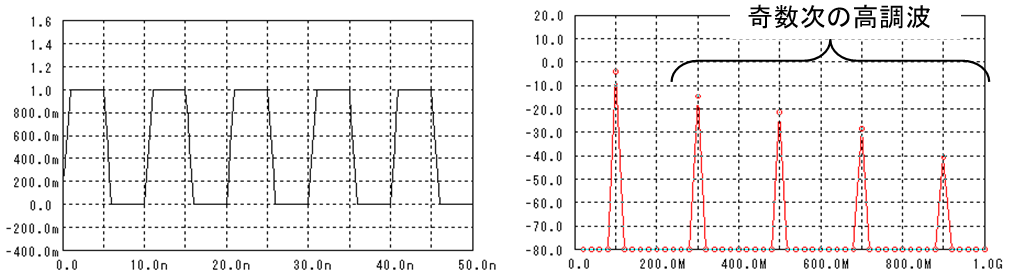
矩形波でも奇数次の高調波が出ますが、その量が三角波のときより多いようです。
(D)矩形波のDutyをずらす
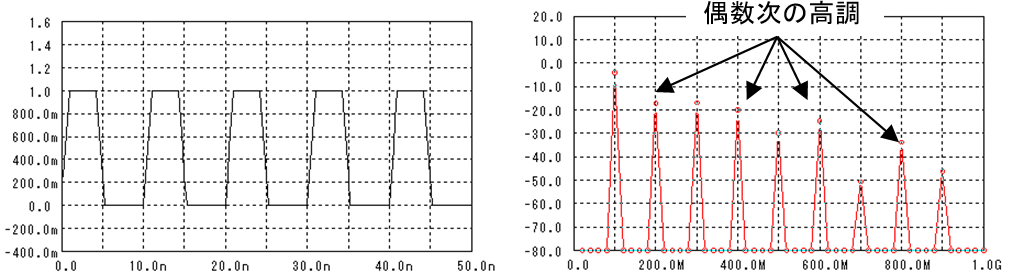
矩形波のDutyを少しずらし(‘1’の時間を少し短くした)ら、偶数次の高調波も出てきました。
ここら辺りまでは、教科書に良く出てきますし、覚えている人も多いと思います。
何でそうなるかについては、色んな本や教科書が触れているのでここでは省略させてください。
(E)複雑化
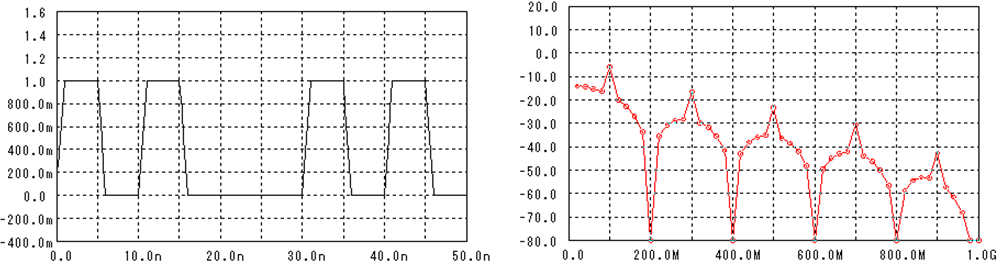
一つだけ‘1’を抜いてみました・・・色々な周波数成分が増えました。
(Dutyは100%に戻しているので、偶数次の高調波は出なくなります)
左の波形は少ししか変化していないのに、非常に複雑な周波数成分を持つことになります。
(F)複雑化(bitをもう一つ抜く)
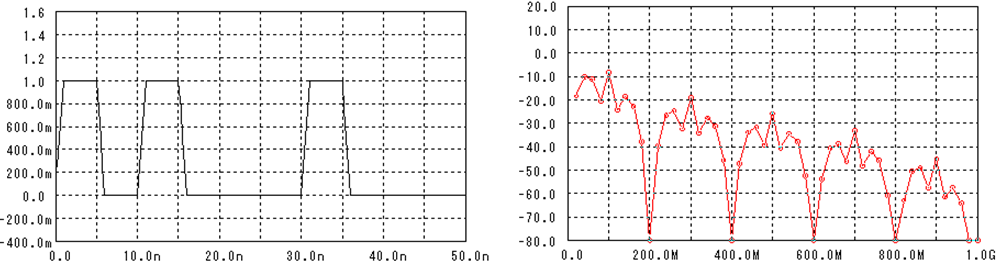
更にもう一つbitを抜くと・・・周波数成分は更に複雑になります。
どんな波形がどんな周波数成分を持っているかを頭で計算(イメージ)できるのは(D)辺りまでで、(E)、(F)は計算機に頼るしかないように思います。
歪みを除くフィルタの設計はアナログ回路の仕事
このアプリを作った目的は、フーリエ変換をするためではなく、フィルタを設計するためです。
アナログ回路の入力される信号は小さくてノイズに埋もれていて、波形も歪んでいることが多いです。そのため雑音の中から必要な信号を取り出し、歪んだ波形を正常に戻すためにフィルタを入れます(これがアナログ回路の仕事です)。
このアプリの目的は、フィルタをどのような周波数特性にしたら良いかを計算することでした。
次回は実際にフィルタを計算で求めて、周波数特性と波形の関係についてもう少し触れたいと思います。