第1章 ΔΣ ADCとは
ΔΣ(デルタシグマ)ADCは、少ない回路構成で高精度(16bit以上)なA/D変換を実現できるA/Dコンバータです。基本構成は、積分器・量子化器(コンパレータ)・ディジタルのフィードバック回路から成り立っており、時間的に平均を取りながら精度を高めるという考え方に基づいています。
◆ナイキスト系ADCとΔΣ ADC
いわゆるナイキスト系ADC(SAR型やパイプライン型など)では、アナログ信号を一定周期ごとにサンプリングし、その瞬間の値をディジタル化します。
高速処理に向いていますが、20bitクラスの高分解能を安定して得るのは難しく、抵抗やコンデンサのばらつき、リファレンス電圧のわずかな揺らぎが誤差の原因になります。

一方ΔΣADCは、「高速で何度もサンプリングし、平均的に正しい値を求める」方式です。
いわば、時間軸を使って精度を稼ぐ現実的なアプローチといえます。
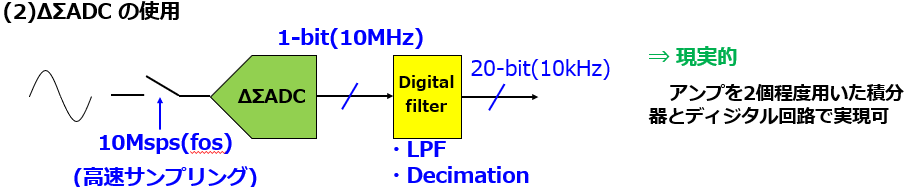
ナイキスト系ADCが10kHzで直接20bit精度を求めるのに対して、ΔΣADCでは、10MHz(10Msps)の高速クロックで1bitデータを出力し、その大量のビット列を後段のディジタル処理で平均化します。
この結果、最終的に20bit相当の高精度が得られます。
ΔΣ ADCの図にある、黄色いブロック「Digital filter」は、ΔΣADCの精度を支える重要な要素です。
このブロックでは、1bit出力を入力として低域通過(LPF)処理と「デシメーション(Decimation)」を行います。
LPFで高周波ノイズを除去し、Decimationでサンプリングレートを落として信号帯域を整えます。
このように、ΔΣADCは「高速サンプリング+ディジタル平均化」によって高精度を達成しているのです。
もう一つの特長は、アナログ部の回路が非常に簡潔で安定している点です。ΔΣ変調器は、オペアンプを使った2段の積分器と1bitの比較器というシンプルな構成で、部品ばらつきや温度変動の影響を受けにくい構造になっています。
そのため、微細化や低電圧動作が進む現在の半導体プロセスでも扱いやすく、IoTセンサーや医療・計測機器など、低消費電力かつ高精度が求められる分野に広く使われています。
◆素子ノイズと量子化ノイズ
さて、A/Dコンバータ(ADC)の出力信号には、さまざまなノイズが含まれています。
ΔΣADCの技術を理解するまえに、素子ノイズと量子化ノイズの違いを知っておく必要があります。

素子ノイズとは、トランジスタや抵抗などの回路素子がもつ物理的なノイズです。
たとえばMOSFETの熱雑音や抵抗のジョンソンノイズなどがこれにあたります。
これらはデバイスが存在する限り避けられないもので、物理的ノイズと呼ばれます。
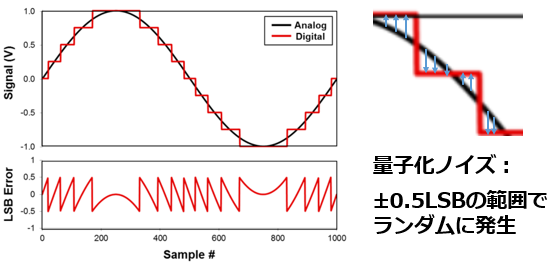
一方で、量子化ノイズは、アナログ信号を有限のディジタル値に変換する際に生じる誤差です。
アナログ入力信号が連続値であるのに対し、ディジタル出力は階段状の離散値でしか表現できないため、その差分が誤差として現れる、システム的なノイズです。
図のように量子化ノイズは±0.5LSBの範囲でランダムに発生し、ADCの分解能が低いほど誤差の幅が大きくなります。逆に分解能を上げ、量子化ノイズを小さくできれば、それだけ高精度なADCが実現できるということになります。
ΔΣADCの設計とは、信号処理と制御理論の考え方で量子化ノイズを小さくすることにあります。
この考え方を実践する上で重要となるアプローチが2つあるので、次章でご紹介します。
◆オーバーサンプリングとノイズシェーピング
ΔΣ ADCにおいて、量子化ノイズを抑えて信号を取り出すアプローチとして、特に重要なものが2つあります。
1つは「オーバーサンプリング(Oversampling)」です。
これは信号帯域よりもずっと高いサンプリング周波数でデータを取ることで、
量子化ノイズを広い周波数範囲に拡散させ、信号帯域内のノイズ密度を下げる手法です。
2つ目は「ノイズシェーピング(Noise Shaping)」です。
ΔΣ ADCの中には積分器が入っており、フィードバックを通じてノイズ成分の周波数分布を変えます。
その結果、信号帯域内のノイズを小さくし、高い周波数に追いやることができます。

この「オーバーサンプリング」と「ノイズシェーピング」を組み合わせ、高速なクロックで1bitデータを生成し、ディジタル処理で多bit精度に変換するというのがΔΣ ADCの基本動作になります。
ちなみにこの2つのアプローチはΔΣ ADC以外でも使えるので、理解しておくとご自身の技術の幅も広がります。
さて次は、ΔΣ ADCの根幹を支えるオーバーサンプリングのアプローチを、量子化ノイズとの関係を交えながら詳しく解説します。
第2章 オーバーサンプリング
◆オーバーサンプリングとは
オーバーサンプリングとは、信号の帯域幅よりもはるかに高い周波数でサンプリングすることです。
通常のナイキスト系ADCでは、信号帯域の2倍の周波数(ナイキスト周波数)でサンプリングを行います。
一方、ΔΣADCでは、数十倍から数百倍もの高い周波数でサンプリングを行います。たとえば、10kHz帯域の信号を扱う場合、ΔΣADCでは100倍の1MHzや、1,000倍の10MHzといったクロックで信号をサンプリングします。
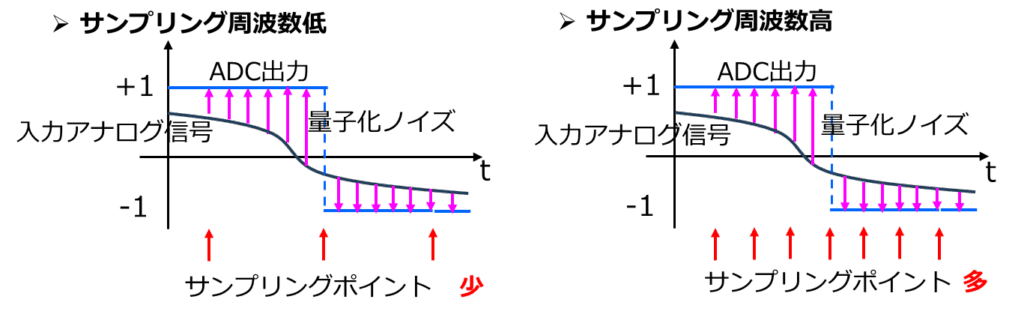
ではなぜ、高い周波数でサンプリングを行うのでしょうか。
・オーバーサンプリングで、ノイズを「薄める」
オーバーサンプリングを行って周波数が変化しても、量子化ノイズの総エネルギーの和は変わるわけではありません。ですからサンプリング周波数が高くなるほど、より広い周波数範囲に量子化ノイズが均等に分布するようになります。つまりノイズが広帯域に拡散し、信号帯域(fs以下)の範囲に含まれるノイズ密度は相対的に小さくなるのです。
これは「ノイズを薄めて信号を取り出しやすくする」と例えれば、わかりやすいかもしれません。
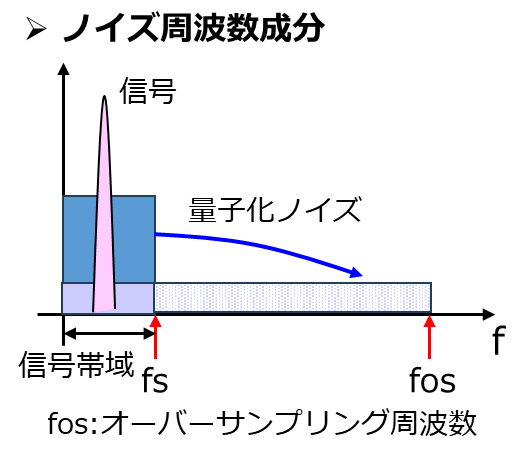
結果的に信号対ノイズ比(S/N比)が向上し、分解能が上がることになります。(但しΔΣ ADC後段のディジタルフィルタでノイズをフィルタリングして落とすことが前提です)

・S/N比の改善量(bit数増加)とオーバーサンプリング周波数との関係
オーバーサンプリングによって得られるS/N比の改善量は、サンプリングポイント数に依存します。
おおまかには、オーバーサンプリング周波数を4倍にすると分解能が約1bit向上することが分かっています。2bit増加させたい場合は周波数は4×4=16倍です。ΔΣADCではこれを活用して手っ取り早くbit数増加を実現できます。
(補足)理解を深めるための補足知識
オーバーサンプリングの効果をより深く理解するには、信号処理の基礎となるウィナーヒンチンの定理とパーセバルの等式の考え方が参考になります。
- ウィナーヒンチンの定理:
信号の自己相関関数とそのパワースペクトル密度はフーリエ変換の関係にある。
つまり、ノイズを時間的にランダム化すると、周波数領域では広帯域に分布することを示しています。 - パーセバルの等式:
信号の全エネルギーは、時間領域と周波数領域で等しい。
これにより、「サンプリング周波数を上げてもノイズエネルギーの総量は一定」という考えが導かれます。
この2つの原理は、オーバーサンプリングがノイズの総量を変えずに分布を変えるという考え方を支える理論的背景です。
ココでは詳述は控えますが、詳細な数式を理解しなくても、
「時間を細かく刻むほど、ノイズが平均化されて密度が下がる」と捉えれば十分です。
次回は、量子化ノイズを抑えて信号を取り出すもう一つの重要なアプローチである「ノイズシェーピング」について、フィードバック制御の観点から解説します。
第3章 ノイズシェーピング
次は、S/N比改善のもう一つのアプローチ、ノイズシェーピングについて解説します。
前章で説明したオーバーサンプリングによって、量子化ノイズは広い周波数帯に拡散し、信号帯域内のノイズ密度が下がることを確認しました。
しかし、オーバーサンプリングだけでは、量子化ノイズは帯域全体に一様に分布したままであり、
帯域内のノイズをさらに下げることはできません。
そこで用いられるのが、「ノイズシェーピング(Noise Shaping)」です。
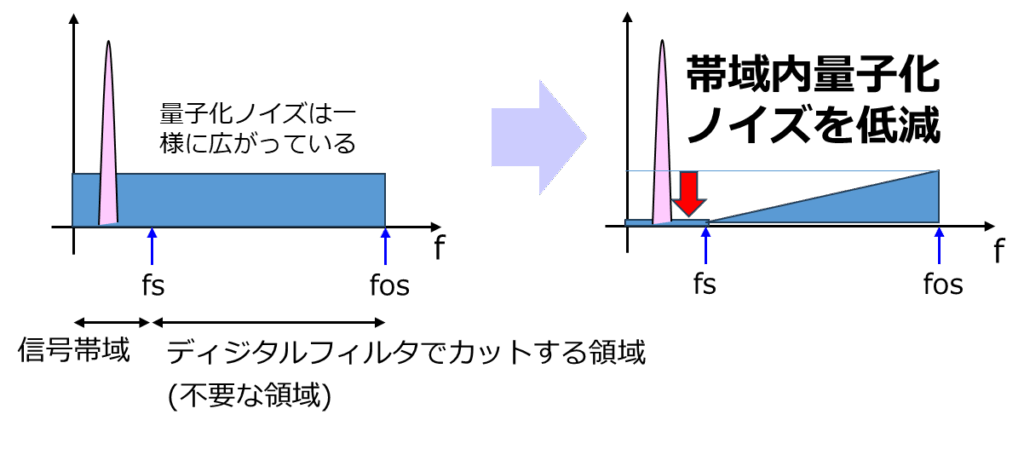
上図の左側は、量子化ノイズが全帯域に均等に広がった状態を表しています。
この状態では、信号帯域(fs以下)にも一定量のノイズが残っています。ノイズシェーピングでは、この信号域内の量子化ノイズをさらに抑圧し、高周波側(fs〜fos付近)へノイズエネルギーを追いやります。
すると、右図に示すように、信号帯域内のノイズが減少します。
このように、ノイズの「量」ではなく「形(周波数分布)」を変えることがノイズシェーピングの目的です。
◆フィードバック制御システムを活用して、ノイズシェーピングを実現
では、どのようにしてこのようなノイズ整形を実現しているのでしょうか。
その鍵となるのが、フィードバック制御システムの原理です。
一般的なフィードバック制御システムでは、入力信号と出力信号の差分(誤差)を取り、その誤差をフィードバックして出力を安定化させます。
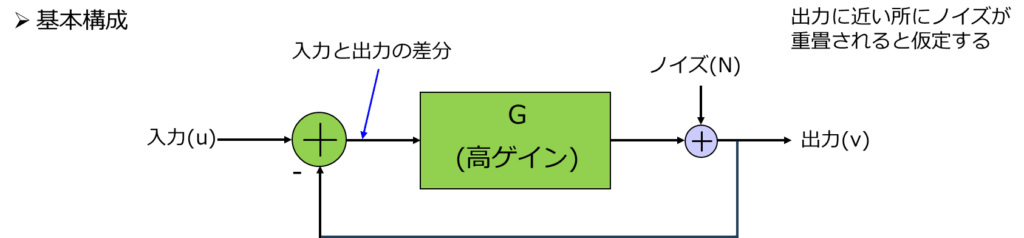
G(ゲイン)が十分に大きい場合、入力信号は正確に出力へ伝達され、一方で、出力側に加わったノイズ(擾乱)は1/G[ゲイン]倍に抑えられます。

この関係は、オペアンプやPLL、DC-DCコンバータなど、多くのアナログ制御回路に共通する基本原理です。
ΔΣADCでは、この制御の仕組みを量子化ノイズの抑圧に応用しています。

量子化ノイズは「出力に付加される擾乱」とみなすことができ、高ゲインな積分器をループ内に配置することで、出力側に生じるノイズ成分をフィードバックで打ち消すことが可能になります。
結果として、信号成分は忠実に通過し、ノイズ成分だけが高周波側へ押し出される――
これがノイズシェーピングの基本動作です。

制御理論の観点で表現すると、ΔΣADCループは「Signal Transfer Function(STF)が入力信号を通過させ、Noise Transfer Function(NTF)が量子化ノイズを抑圧して通さない」という構造になっています。
ループ内のフィルタ(積分器)は低域で大きなゲインを持つため、低域の量子化ノイズは大きく減衰し、結果的に帯域内S/N比が劇的に改善します。
オーバーサンプリングによってノイズを広帯域に拡散し、ノイズシェーピングによって信号帯域内のノイズ成分だけを制御的に削る――
この二つの効果が重なることで、ΔΣADCは非常に高い分解能を達成しています。ΔΣADCにおけるノイズシェーピングは、フィードバック制御理論をA/D変換に応用した代表例といえます。
この章では、ノイズシェーピングが「量子化ノイズの分布を制御するアプローチ」であり、その実現がフィードバック制御システムに基づいていることを説明しました。次章では、実際のΔΣADCの構成要素――積分器・比較器・ディジタルフィルタなど――を取り上げ、これらのブロックがどのように連携して高精度を実現しているのかを見ていきます。
第4章 ΔΣADCの構成要素
前章では、ΔΣADCの振る舞いが「フィードバック制御系」と同じ原理で動いていることを説明しました。
本章では、そのフィードバックループを構成する具体的なハードウェア要素について整理します。
ΔΣADCは、「少ないアナログ回路で高精度を実現する」という特徴を持っています。
構成要素は大きく 積分フィルタ(積分器)・コンパレータ・ディジタルフィルタ の3つです。
これらがループを形成し、量子化ノイズを制御的に抑圧する仕組みをつくっています。
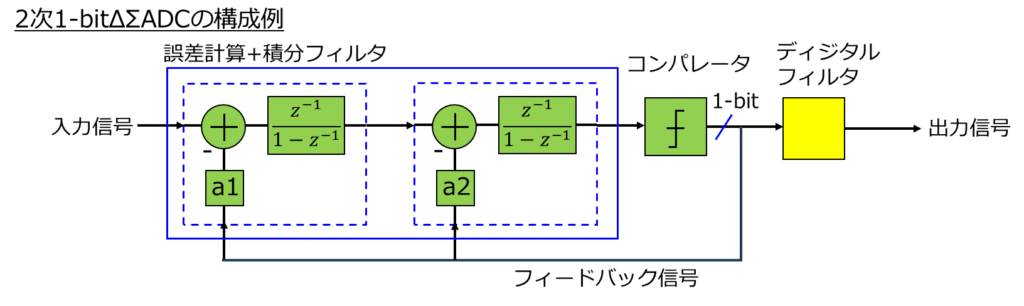
図 2次1-bit ΔΣADCの構成例
(積分器2段+1bit量子化器+ディジタルフィルタで構成される基本モデル)
1. 積分フィルタ(積分器)(Integrator)
積分器は、ΔΣADCのノイズシェーピングを生み出す中心要素です。
入力信号とフィードバック信号(a₁・a₂)の差分(誤差)を蓄積し、その結果を次の段へ渡します。
上図にある「1 / (1 − z⁻¹)」のブロックが積分器を表しており、ノイズシェーピングを行う次数に応じた数の積分器を搭載します。これが2段構成となると「2次のΔΣ変調器」になります。
積分器の段数(次数)を増やすほど帯域内ノイズは強く抑圧できますが、同時にループ不安定性も増すため、実用範囲は2〜4次が一般的です。
2. コンパレータ(量子化器)
積分器からのアナログ値は、コンパレータ(量子化器)で1bitディジタル値に変換されます。
ΔΣADCにおける量子化器は、
- アナログ値を1bit(0/1、または+1/−1)へ変換
- ここで発生する量子化ノイズをループで整形(ノイズシェーピング)
という2つの役割を担います。
構造が単純でばらつきにも強いため、多くのΔΣADCは1bit量子化を採用しますが、高性能用途では2bit〜3bitの量子化器を使う構成もあります。
3. ディジタルフィルタ
コンパレータ(量子化器)からは高速の1bitデータ列が出力されますが、
このデータは帯域外ノイズを多く含んでおり、そのままでは利用できません。
そこで、ディジタルフィルタが以下の処理を行います:
- LPF(ローパスフィルタ):高周波ノイズを除去
- Decimation(デシメーション):サンプリング周波数を下げ、信号帯域だけを抽出
ディジタルフィルタの形式としては、CICフィルタやCIC + FIRフィルタの組み合わせがよく使われ、
性能とハードウェア効率のバランスが取れる構成になっています。
このように、ΔΣADCは、
- 積分器:ノイズを整形する中心要素
- コンパレータ:アナログを1bit化
- ディジタルフィルタ:帯域外ノイズを除去し高精度データを生成
という3つの要素が一体となって、大きなフィードバックループを持つ制御回路の一種として動作しています。
さて、次はΔΣ ADCのシステム設計についてご紹介します。
第5章 ΔΣADCのシステム設計
◆設計は“手順”がすべて
ΔΣADCの設計では、いきなり回路を作り始めると必ず行き詰まります。その理由は、ΔΣADCが「アナログ回路」「ディジタル処理」「制御理論」が混ざったシステム設計そのものだからです。
したがって最初に、全体構成を決めるための手順をしっかり踏む必要があります。

① 仕様の決定
ΔΣADCの設計で最初に決めるべきは、
最終的に必要となる 分解能、サンプリングレート、SNR、帯域幅(BW) といった基本仕様です。
ここで決まる数値が、後続の
- OSR(オーバーサンプリング比)
- 変調器の次数
- NTF(Noise Transfer Function)の形状 にすべて影響します。
仕様決めは「何bitが必要か?」だけではなく、
何Hz帯域が必要で、どの程度のノイズフロアを許容できるのかを含むため、アプリケーション要求と密接に結びついています。
② オーバーサンプリング比(OSR)・次数の選定
必要な分解能とSNRが決まったら、それを満たすためのOSR(オーバーサンプリング比) と 変調器の積分次数(1次〜4次) を選びます。
一般的には、
- OSRを上げるほどS/N比は改善しやすい
- 積分次数を上げるほど帯域内ノイズを強く抑圧できる(ノイズシェーピングが強くなる)
という関係があります。
ただし、OSRを極端に上げると消費電力やデジタル負荷が増え、次数を上げるとループ安定性が悪化するため、この2つは設計者が慎重にバランスを取る必要があります。(後で詳述します)
③ ノイズ伝達関数(NTF)計算
OSRと次数が決まったら、NTF(Noise Transfer Function:量子化ノイズがどのように通過するか) を設計します。
NTFの形が、ΔΣ変調器の
- 安定性
- 帯域内ノイズ量
- 雑音シェーピングの強さ
を決定づけます。
この段階では、シミュレーションツールや数学的解析を用いて安定で目的の性能を満たすNTFを求めることが重要となります。
④ モデル作成および特性検証(Modeling & Simulation)
NTFまで決まったら、ようやくシミュレータモデルを使い回路を動かす段階に進みます。
- Verilog-A
- MATLAB / Simulink
- Pythonモデリング
- スイッチトキャパシタ回路の抽象モデル
などのシミュレータを使い、ΔΣ変調器のモデルを作成します。
次章では、それぞれの工程(①〜④)を1章ずつ掘り下げて解説していきます。
第6章 仕様の決定
前章で示したように、ΔΣADCの設計は 「仕様 → OSR・次数 → NTF → モデリング」 の順で進めることが重要です。このうち最初のステップである「仕様の決定」は、後続の設計全体に影響するもっとも重要な工程です。
ここで求められるのは、単なる「〜bitが欲しい」という要求だけでなく、帯域・SNR・最大入力といった総合的な性能要件を整理することです。
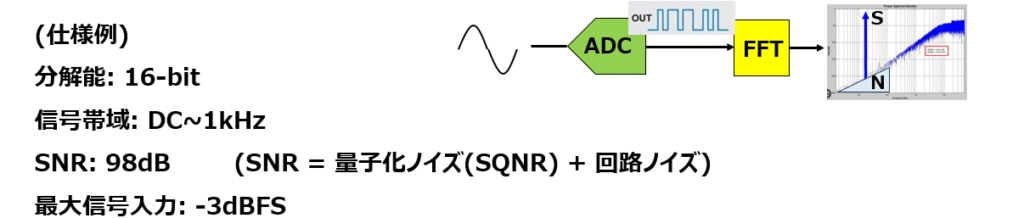
仕様例を上記に示しました。この仕様例を元に、代表的な4つの使用項目について説明します。
①分解能(Resolution)
まず求められるのは、最終的に達成したいディジタル分解能です。ここでは 16-bit を目標としています。
ただし、ΔΣADCでは「量子化bitの数 = 出力分解能」ではありません。1bitまたは数bitの量子化器からスタートし、OSR(オーバーサンプリング比)とノイズシェーピング効果により16-bit相当の性能を作り上げます。
このため、後の章で扱う OSR や NTF を設計するための“目安”となる項目です。
②信号帯域(BW: Signal Bandwidth)
今回の例では DC〜1kHz を対象帯域とします。この帯域が広いほどサンプリング周波数(fos)への要求が高くなり、OSRの選定にも直接影響します。
ΔΣADCは「高精度・低帯域」用途に向いているため、1kHz程度の帯域は典型的なユースケースといえます。(低消費で高分解能が求められるため、医療・計測・IoT用途と親和性が高い帯域です)
③SNR(Signal-to-Noise Ratio)
今回の仕様では SNR = 98 dB を目標値としています。
ここで重要なのは、SNRが 量子化ノイズ(SQNR)+アナログ回路ノイズの合計 で決まる点です。
ただしΔΣADCの設計初期では、
- 物理ノイズ(抵抗熱雑音など)
- 回路ノイズ(アンプの入力換算ノイズなど)
をすべて正確にモデル化して評価するのは困難です。
そこで設計初期段階では、
量子化ノイズだけを取り出した SQNR を基準に SNR を概算します。
SNR(dB)≈6.02B+1.76SNR(dB) \approx 6.02B + 1.76SNR(dB)≈6.02B+1.76
は理想的な量子化ノイズのSNRであり、B に 16bit を代入すると約 98 dB となります。
今回の設計例では、「回路ノイズはSQNRより十分小さく抑える」という前提のもと、SNR ≒ SQNR として 98 dB を目標値に設定しています。
④最大入力レベル(Input Range)
最大入力は –3 dBFS(Full Scale) に設定されています。
これは実際の信号がクリッピングする余裕(ヘッドルーム)を確保するための設定で、
後段のFFT解析や実装時のダイナミックレンジ確保にも影響します。
ΔΣADCでは、入力信号のレベル設定が
- 積分器の内部状態
- ループの安定性
- SNDR(Signal-to-Noise-and-Distortion Ratio)
に強く影響するため、この値を適切に設定することが重要です。
次章では、この仕様を用いて、オーバーサンプリング比(OSR)と変調器の次数の決め方
について具体的に解説していきます。
第7章 オーバーサンプリング比(OSR)と変調器の次数の決め方
前章で設定した仕様では、ΔΣADCとして SNR = 98 dB を達成する必要があります。
この目標を満たすためには、
- オーバーサンプリング比(OSR)をどれだけ大きくするか
- 変調器の次数(1〜4次)をどう選ぶか
を適切に決める必要があります。
この説明をするために、群馬大のアナログ技術シリーズの解説がとても分かりやすかったので、引用させていただきました。
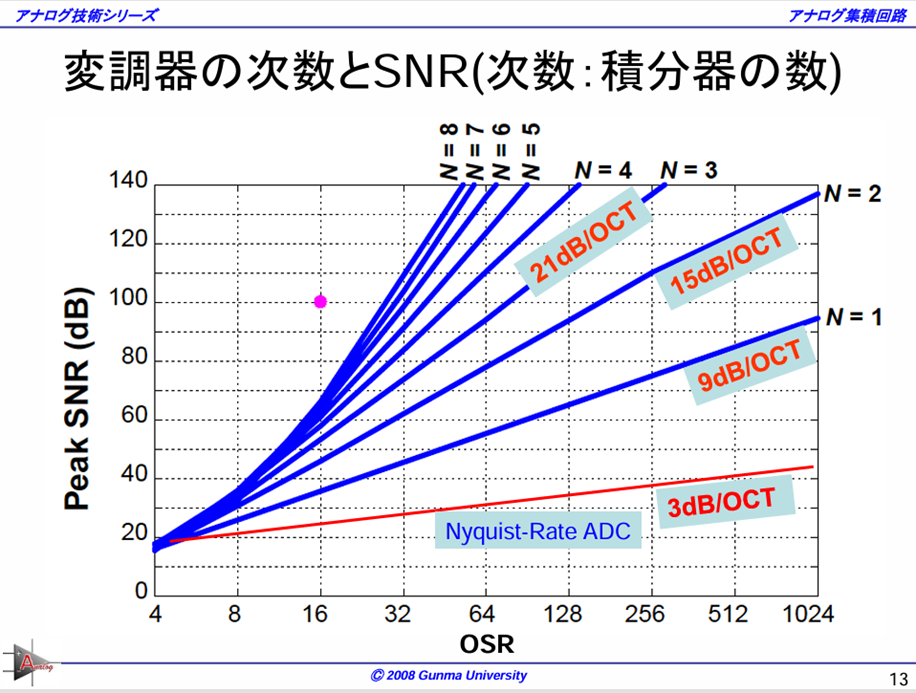
ΔΣ変調器では次数が1段上がるごとに帯域内ノイズの低減量が大きくなるという特徴があります。
図の傾きに書かれている
- 1次:9 dB/Oct
- 2次:15 dB/Oct
- 3次:21 dB/Oct
という数字は、「OSRを2倍にしたときに何dB SNR が改善するか」を表しています。
◆98 dBのSNRを得るためのOSR候補
図の曲線から、SNR = 96〜98 dB を達成するためのOSRと次数の組み合わせを読み取ると、代表的には次の2つが候補として挙げられます。
(A)OSR ≈ 100、3次(N=3)
(B)OSR ≈ 200、2次(N=2)
(A) 3次変調器はノイズシェーピング効果が強く、OSRが100程度でも約100 dB前後のSNRが得られます。
ただし、デメリットとしてループが複雑になり安定性確保が難しい、高次になるほど係数調整の難易度が上がる、という設計上の課題があります。
一方(B) 2次変調器では、OSR=200付近で100 dBに達しますが、2次は設計が比較的安定で扱いやすく、アナログ回路も簡潔にできるというメリットがあります。
ここで、実装可能なクロック周波数 fos を 1 MHz 程度 と仮定すると、次の計算でOSRが求まります。
信号帯域(前章):1 kHz
OSR = fos / (fs/2) = 1 MHz / (2 kHz) = 500
本システムではOSR ≈ 500 が実現できる条件になるため、実装可能なクロック周波数や特性(2次の青いライン)から見て、(B)の2次変調器で十分に98 dB を達成できそうです。
最終的に採用する構成は以下のとおりとなりました:
◆ΔΣADC構成
- 次数:2次
- OSR:500
- fos(変調器動作周波数):1 MHz
第8章 ノイズ伝達関数(NTF)計算
前章ではオーバーサンプリング比(OSR)と変調器の次数を決めました。
次に行うべき工程が ノイズ伝達関数(NTF:Noise Transfer Function)の設計です。
NTFは、ΔΣ変調器の「ノイズをどう通し、どう抑えるか」を数学的に表したものです。言い換えると、量子化ノイズをどの周波数帯へ押し出すか を直接決めるのが NTF です。
◆NTFがなぜ必要か
3章のノイズシェーピングの所で少し触れましたが、ΔΣADCでは、量子化ノイズを
- 信号帯域内(低周波):抑圧したい
- 帯域外(高周波):押し出したい
という目的でフィードバック制御を行います。
この「周波数ごとのノイズの通りやすさ」を示すのが NTF です。NTF がうまく設計されていれば、帯域内のノイズ量は非常に小さくなり、SNR が大幅に改善します。
逆に、NTF の形が適切でないと、
- ループが不安定になり発振する
- 理論値通りの SNR が出ない
- 過大な内部信号が発生しオペアンプが飽和する
といった問題が起こります。
つまり、NTF は ΔΣADC の性能と安定性を左右する“要”の1つと言えます。
◆制御理論から導かれる NTF の基本式
ここで再び3章のノイズシェーピングでご紹介した式の登場です。ΔΣ変調器はフィードバック制御系と同じ構造を持っており、そのループゲインを H(z) とすると、出力は次の形で表されます:
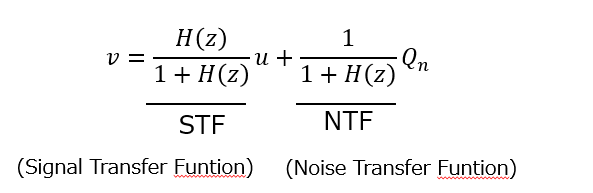
この式の後半部分 が、量子化ノイズへの影響(ノイズ伝達関数)を表した項になります。
STF と NTF
- STF(Signal Transfer Function) = H(z) / (1 + H(z))
→ 入力信号がどれだけ通るか - NTF(Noise Transfer Function) = 1 / (1 + H(z))
→ 量子化ノイズがどれだけ通るか
ΔΣADCでは STFはほぼフラット(=信号はそのまま通す)
NTFは高周波でノイズが通りやすくなる形状 を目指して設計します。
◆NTFの設計方針:次数と形をどう決めるか
前章で決めたように今回の構成は
- 次数:2次
- OSR:500
- 目標SNR:98 dB
ですので、必要なNTFの性質は次の通りです。
① 2次のノイズシェーピング
2次のΔΣでは、NTFはおおよそ

という形を持ちます。これは、
- 低周波(z ≈ 1)で NTF ≈ 0 → ノイズは強く抑圧
- 高周波では NTF が急激に上昇 → ノイズを帯域外へ押し出すことを意味します。
② OSR=500 に応じたフィルタ形状
OSRが十分大きい場合、帯域内ノイズは NTF の次数でほぼ決まります。
今回の構成(2次・OSR=500)では計算上、98 dB 以上のSNRが得られる NTF を設計可能です。
◆NTF設計時の注意点
NTFは強力なノイズシェーピング効果を生み出しますが、同時にループの安定性にも影響するため注意が必要です。
主な注意点は以下の3つです:
- 内部信号の振幅が大きくなりすぎないこと:次数を上げたり NTF の形を急峻にしすぎると、積分器内部の信号が飽和し、実回路で破綻します。
- 極(Pole)の配置:NTF から逆算される H(z) の極配置が不安定領域に入らないようにする必要があります。
- 実回路の素子ばらつきの影響:NTF が理想的でも、アナログ部分のばらつきで想定通りのゲインが確保できない場合、安定性が損なわれるため、係数 a₁, a₂ などの調整が重要です。
次章では、この NTF に基づく ΔΣ変調器モデルを実際に作り、波形シミュレーションで性能を確認する工程について説明します。
第9章 モデル作成および特性検証
前章までで、ΔΣ変調器の構成要素・OSR・次数・NTF設計がすべて整いました。次に行う工程が モデル化(Modeling)と特性検証(Simulation) です。
ΔΣADCはアナログ回路・ディジタル処理・制御理論が混在するため、いきなり回路設計を始めても思った通りの性能が得られないことがほとんどです。そのため、実回路に着手する前に、抽象モデルを作成して特性を確認することが重要です。
今回の設計では、Verilog A等を用いて ΔΣ変調器の2次モデルを構築し、入力信号に対してどのような 1bit 出力が得られるかを確認しています。
◆時間波形で見るΔΣ変調器の振る舞い

青線が入力アナログ信号(例:微小な1kHzの正弦波)、赤線がΔΣ変調器の 1bit 出力 です。
1bit 出力は 0 / 1(または ±1)を高速に切り替えますが、その切り替わりの頻度(=出力デューティ)が入力信号に対応しています。
入力信号が上昇すると1bit出力の “1” の密度が増え、入力信号が下降すると “0” の密度が増えるため、
この密度情報を後段のディジタルフィルタが取りまとめることで、アナログ値相当の情報が得られます。
◆FFT波形で見る量子化ノイズのシェーピング

赤線が1bit出力の周波数スペクトル(FFT)です。図を見ると、次の特徴が確認できます。
■ 信号成分(ピーク)
約1kHz付近に鋭いピークが見えており、入力のサイン波が正しく変調の中で保持されていることがわかります。
■ 量子化ノイズの帯域外への追い出し(ノイズシェーピング)
FFTの低周波側(信号帯域)ではノイズが大きく抑圧され、高周波側に向かってノイズが増加していることが分かります。図の青色で塗られた領域が 量子化ノイズ であり、これは前章で説明した NTF の働きにより帯域外に押し出されていることを示しています。
これは ΔΣADC のもっとも重要な特徴であり、帯域内ノイズの低減 → 高SNR の実現 に直結します。
◆ここまで検証したら、回路設計へ
今回の例では、時間波形・FFT波形から 2次・OSR=500 の構成で設計仕様(98 dB SNR)が達成可能
であることがモデルシミュレーションで確認できています。
モデルシミュレーション検証は、ΔΣADC設計における重要ステップです。時間波形で ΔΣ変調器の動作を、FFTでノイズシェーピング効果を可視化することで、設計したOSR・次数・NTFが妥当であるかを確認できました。
本稿ブログのシリーズも長くなりましたので、回路設計はまた機会があればご紹介したいと思います。では最後に、ΔΣ ADC システム設計でのポイントをまとめます。
◆まとめ
本稿では、ΔΣADC(デルタシグマA/Dコンバータ)について、その「基本概念」と「システム設計の手順」を段階的に解説してきました。
前半で、ΔΣADCが
- 少ないアナログ回路で高精度を得られるA/D変換方式であること
- オーバーサンプリングとノイズシェーピングが性能向上の鍵であること
- 制御理論(フィードバック)の応用として理解できること
を紹介。ΔΣADCがどのような仕組みで高精度を実現しているのかを押さえました。
また後半では、実際の設計に向けて
- 仕様の決め方(分解能・帯域・SNRなど)
- OSRと次数の選定方法
- NTF(ノイズ伝達関数)の考え方
- モデル構築とシミュレーションの重要性
といったシステム設計手順を順に整理しました。
◆ΔΣADCは今後ますます重要になる技術
ΔΣADCは、計測、通信、音響、医療機器、IoT センサーなど、低消費電力で高精度が求められるあらゆる分野で広く活用されています。近年の半導体プロセス微細化が進む中で、「アナログ+デジタル処理で性能を作り込む」という ΔΣADC の思想は、今後さらに価値が高まると考えられます。
もし今まで「ΔΣADCは難しそう」と感じていたとしても、
ここまで読み進めてくださった読者であれば、設計の入口に立てる知識 を身につけています。これを機に、ぜひご自身で“小さな一歩”から始めてみてください。
ΔΣADCは、深く学べば学ぶほど面白い世界です。
本稿がその第一歩となれば幸いです。