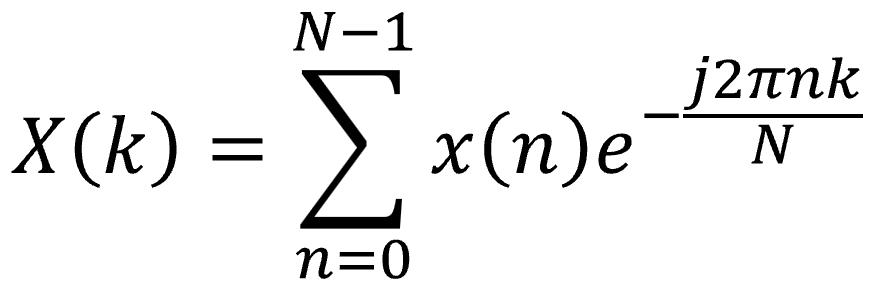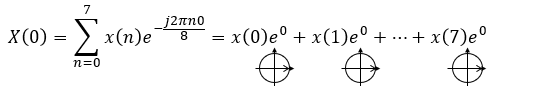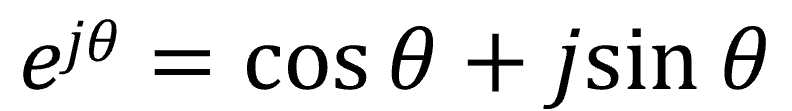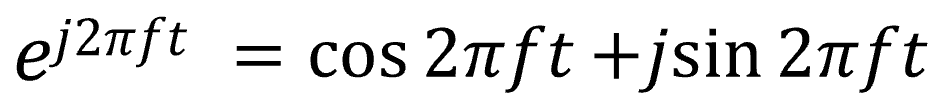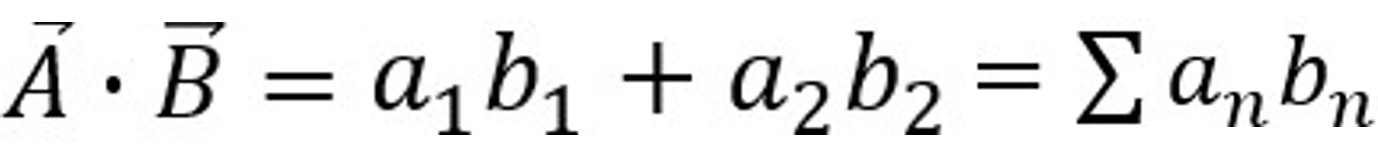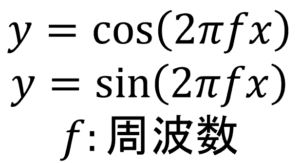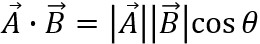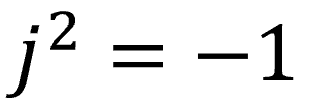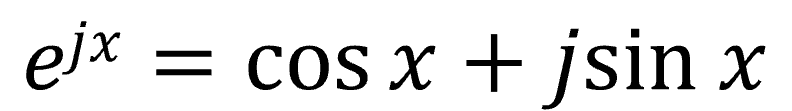こんにちは、狂右衛門(くるえもん)です。 前回、フーリエ変換の得意技は「連続的な信号を離散的な周波数成分に分解することで、時間領域の信号から周波数領域に変換」すること、またディジタル信号の周波数特性を解析し、特定の周波数成分のフィルタリングや圧縮などの処理が可能になるとお伝えしました。 今日は離散フーリエ変換の数式と前提知識についてお伝えします。 離散フーリエ変換の数式 離散フーリエ変換の数式はこ […]
こんにちは、狂右衛門(くるえもん)です。
前回、フーリエ変換の得意技は「連続的な信号を離散的な周波数成分に分解することで、時間領域の信号から周波数領域に変換」すること、またディジタル信号の周波数特性を解析し、特定の周波数成分のフィルタリングや圧縮などの処理が可能になるとお伝えしました。
今日は離散フーリエ変換の数式と前提知識についてお伝えします。
離散フーリエ変換の数式
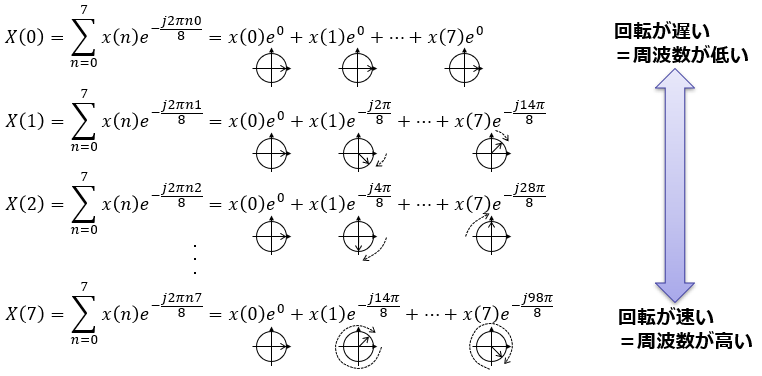
離散フーリエ変換の数式はこれです。
第一印象はどうお感じになりましたか?
私が離散フーリエ変換について講義する際に、数式をご覧になった参加者からの反応はこんな感じです。
とっつきにくいと感じられた方が多いようですね。。。でも、このような問いに私はいつも「大丈夫ですよ」とお答えしています。このブログシリーズでも、そのことをお伝えしたいと思います。
離散フーリエ変換(DFT)4つの前提知識
さて、今回は離散フーリエ変換(DFT)を知る上で前提となる、高校で習ったけどおそらく社会人になっても使わないと思っていた数学知識が3つと、有名な公式1つについてお伝えします。昔皆さんが学校で習った(はず)記憶を引っ張り出してみましょう。
①三角関数
1つ目は三角関数です。cosとかsinというやつです。私がこれを高校で習った時には、正直「三角関数なんて何の役にも立たない!」と本気で思っていましたが、ディジタル信号処理では非常によく使います。
その理由は、三角関数のcosやsinの波の形が、ディジタル信号処理で扱う信号=周期的な波の形にとても似ているからです。とても似ているので、三角関数はディジタル信号処理に便利に扱えるわけです。
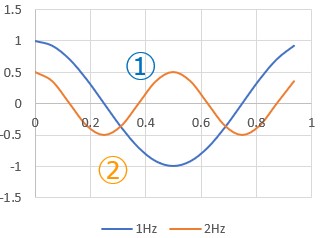
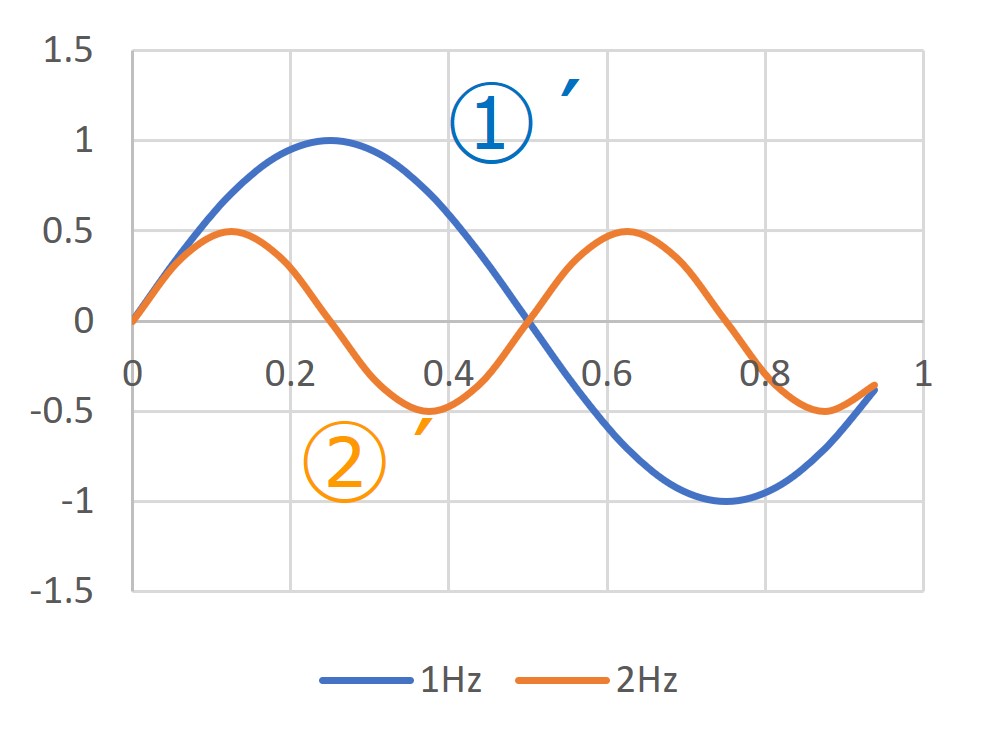
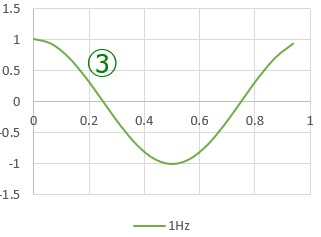
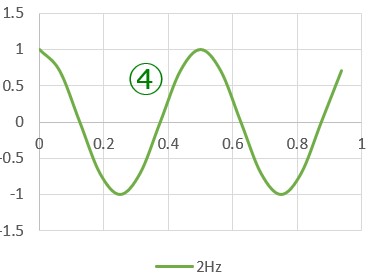
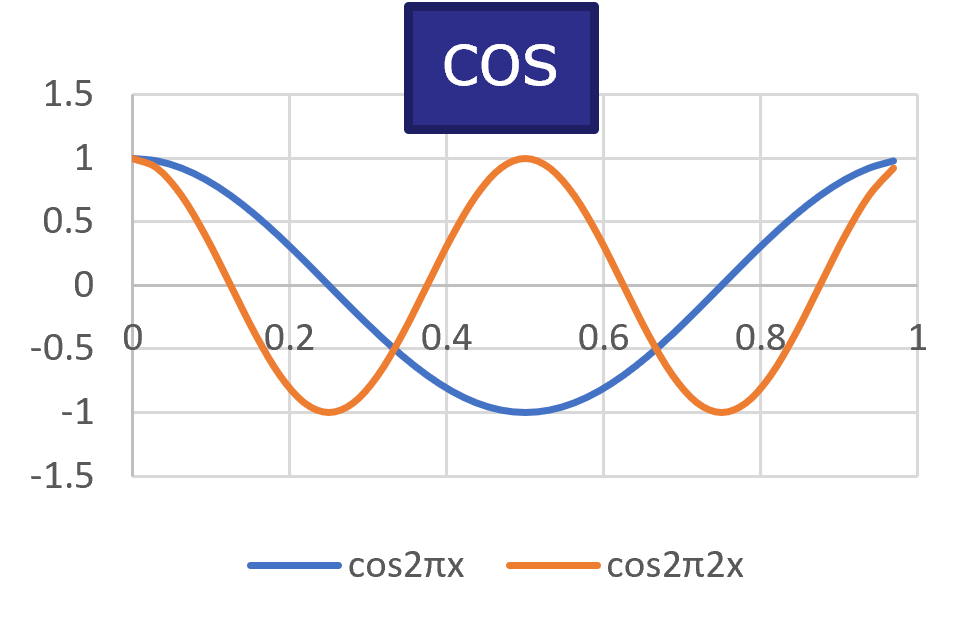
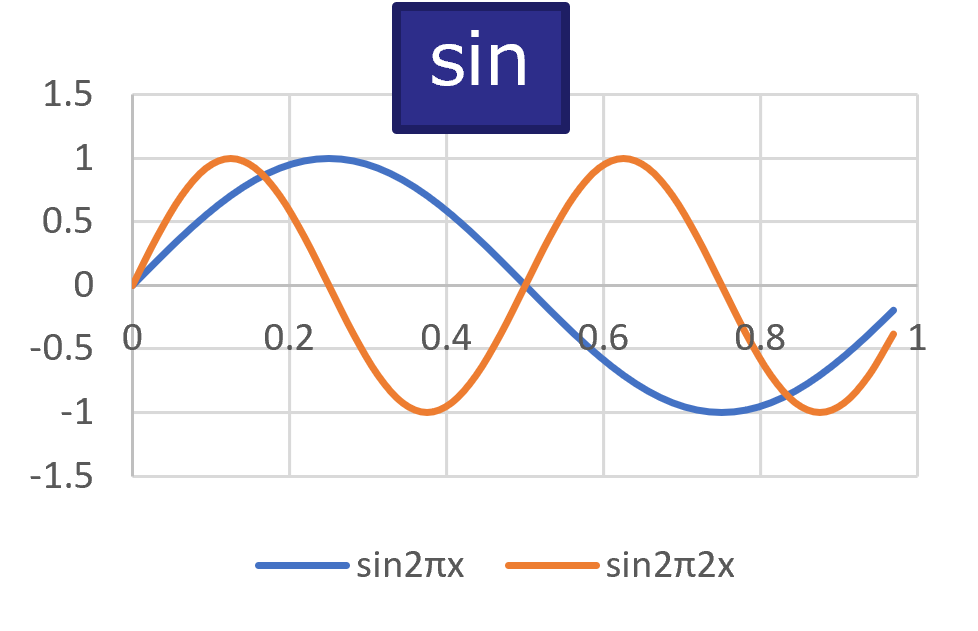
三角関数のcos(余弦波)とsin(正弦波)の例を示してみました。
図1
次に図2に信号=周期的な波の形を平面図で表現し、信号処理でよく扱う事象を表しました。信号の波の高さを振幅、1秒間に繰り返す波の数のことを周波数f、繰り返す波のどこにいるのか位置情報を位相と呼びます。三角関数と形がとても似ていますね。
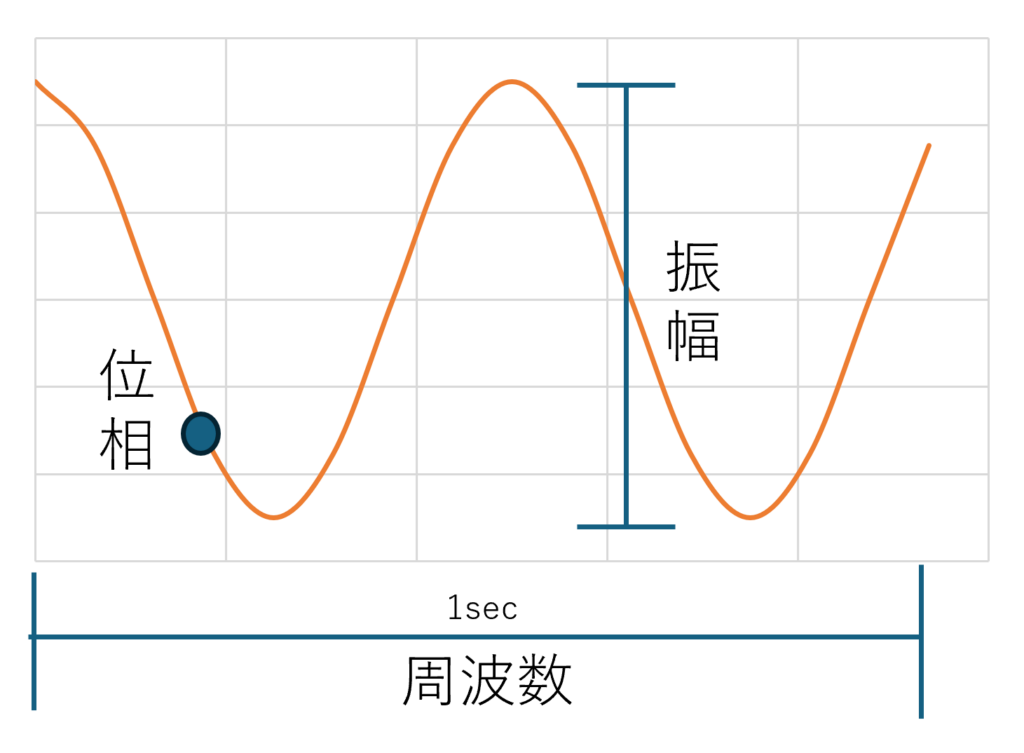 図2
図2
形が似ているので、三角関数は信号処理の基本的な構成要素が扱え、信号の振幅、周波数、位相を表すのにとても役立ちます。
余談ですがcosとsinは数学ではそれぞれ余弦波、正弦波と言いますが、ディジタル信号処理の世界ではどちらも正弦波と言います。おそらく位相(周期的に変動する波の位置情報や振動するタイミング)が異なるだけだから、偉い先人がシンプルに同じ言い方にしたのだろうと勝手に思っています。
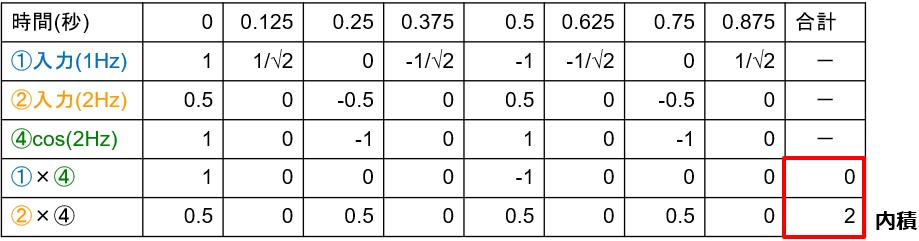
②内積
2つ目は内積です。これも当時三角関数以上に何に使うのかサッパリ理解できませんでした。
内積は「2つのベクトルAとBがどれだけ似ているか=相関」を求めるものでしたね。ベクトルAとBの内積は、2つのベクトルの大きさとそれらの間の角度θのcosの積として表せます。このような公式です。
平面図で表すとこんな感じです。
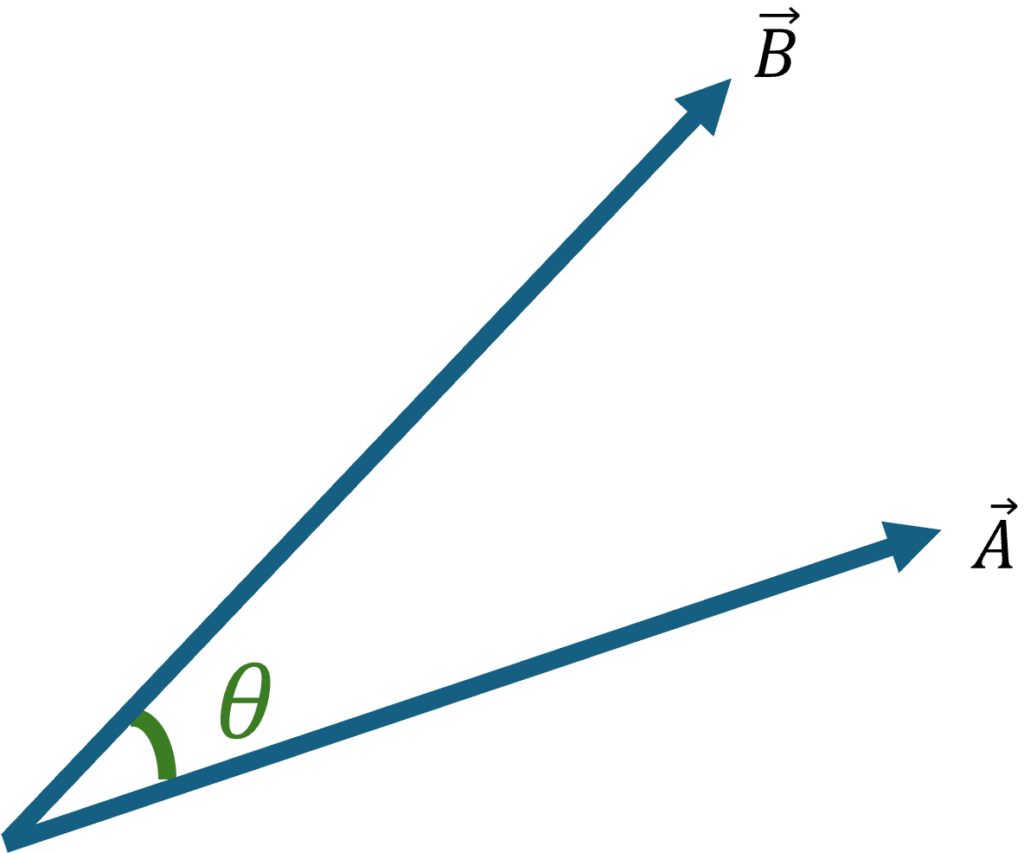 図3
図3
次にベクトルAとBを成分表示してみます。xyの2次元でベクトルAの成分は(a1,a2)、ベクトルBは (b1,b2)としてグラフで表すと図4のような感じになります。
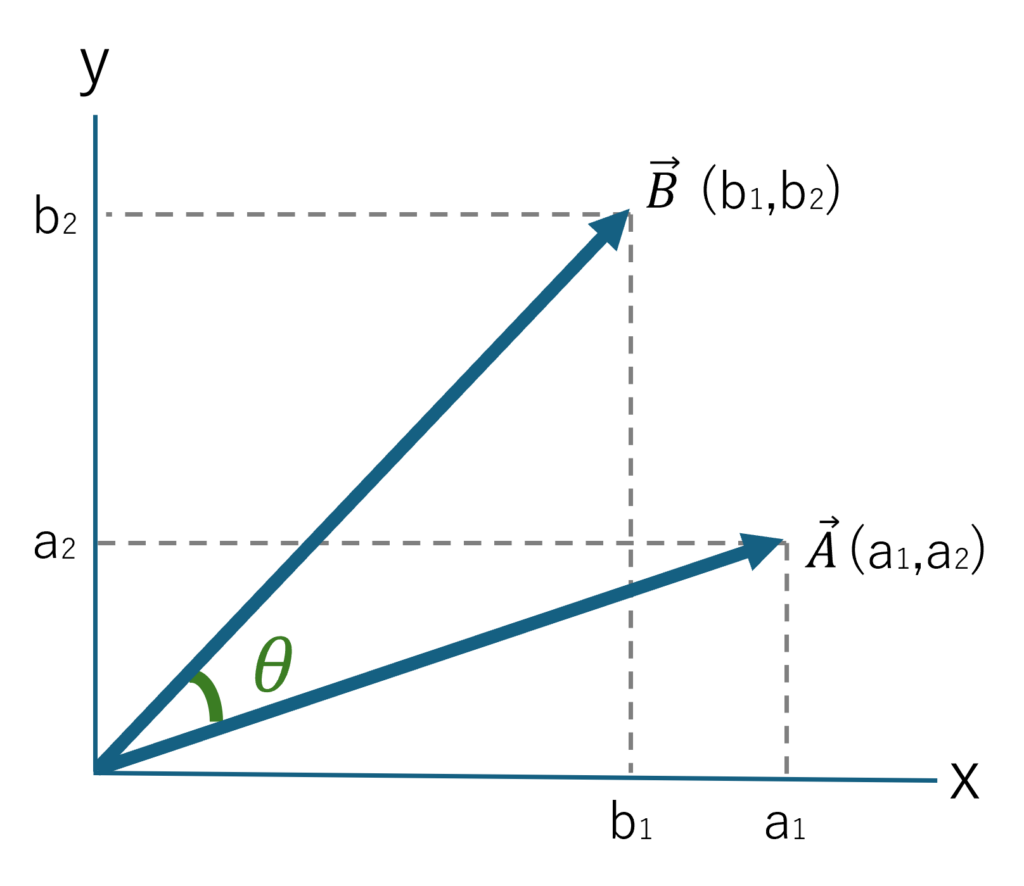 図4
図4
このときベクトルAとBの内積は各成分の積の総和としても表すことができます。式で書くとこうなります。(次元がn個に増えても考え方は変わりません)
図5は、左図に内積のベクトル成分値(a1,a2),(b1,b2)を、右図で横軸をn、縦軸を各成分の大きさとして、並べ変えてみました。
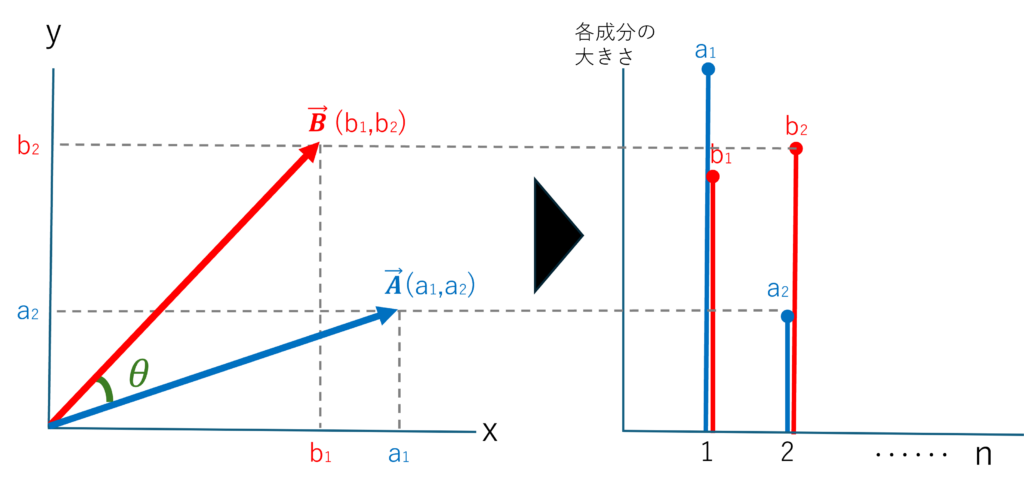 図5
図5
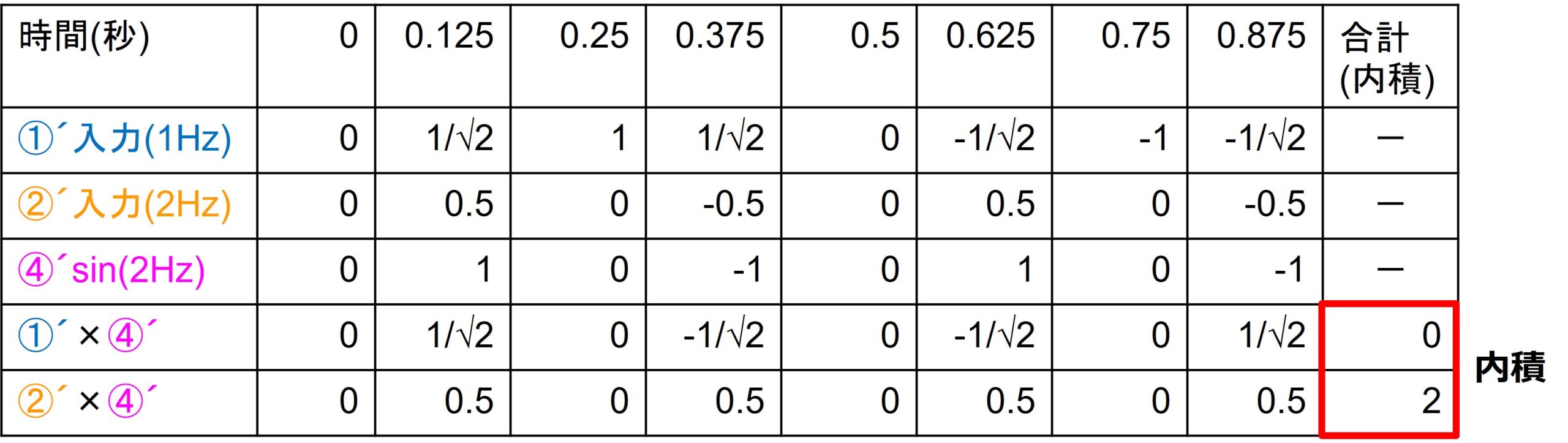
この時、各成分の積 a1×b1+a2×b2+…an×bnの和が、内積になります。
ベクトルを信号とみなせば、左図は、信号に含まれる成分の大きさで、それを時間nで離散的に示せることわかる思います。また、内積は信号AとBの相関を求めていることと同じになります。
③虚数
高校で習ったけどおそらく社会人になっても使わないと思っていた数学知識の3つ目は虚数です。2乗すると-1になる謎の数字です。これも一生使うことはないと思っていましたが、ディジタル信号処理では虚数をよく使います。
ディジタル信号処理では、高校数学では虚数をiで表しますが、信号処理では、iが電流と間違えやすいためjを使います。
信号処理では、実数だけで信号の計算すると場合分けが発生するため計算がかなり面倒です。虚数が加わることで実数だけの計算よりも手早く信号の特性を分析できます。実際にはこの虚数と実数の両成分を合わせ持つ複素数を使うことで、信号の振幅と位相情報を手間をかけずに算出できるようになります。
④オイラーの公式
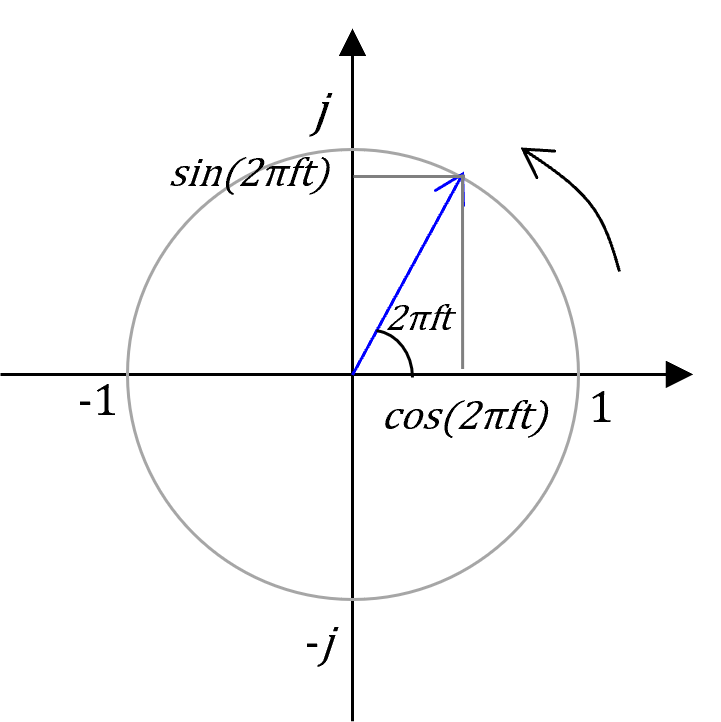
最後、4つ目はある有名な公式です。三角関数と指数関数の関係を表す式、オイラーの公式です。
 オイラー様 (wikipediaより)
オイラー様 (wikipediaより)
信号処理の計算は冒頭の三角関数を用いれば可能ですが、指数関数を使うと計算がより簡単になるので扱い方を覚えておくと便利です。その計算方法も追ってご紹介いたします。
以上、高校では役に立たないと思っていたが、今とても役立っている数学知識を中心にお伝えしました。皆様も思い出してきましたでしょうか。将来息子が高校で習い始めたら「使えるのでしっかり覚えとけ!」と心からアドバイスします笑
次回は周波数成分の求め方をお伝えします。理解が進むように例や図解を用いて解説を進めますね。
ディジタル信号処理の伝道師。
そっと秘密の道具を差し出してクライアントのピンチを救う、
あのネコ型ロボットのようなエンジニアが理想です。