前回までは“反射”がどの様に波形に影響を与えるか過渡解析を使って説明をしてきました。今回は小信号解析（AC解析）も使ってもう少し反射について説明したいと思います。

過渡解析を使わず、AC解析を用いる

線形解析ができるのか確認

“反射”と言うと進行する波と反射する波があり、それらが重なり合うので、なんとなく線形解析が出来ないような気がするのですが、どうなるか確認してみたいと思います。

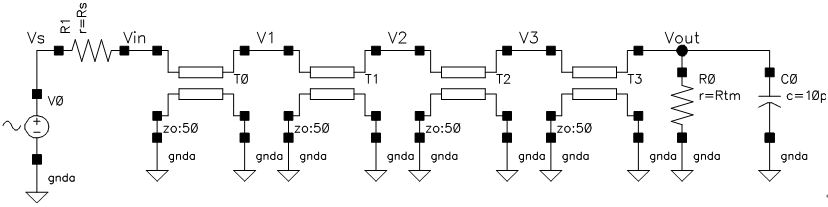
前回使った回路を図 1に示します。信号源インピーダンスRs=40Ω（多重反射を意図的に発生させます）で、終端側の抵抗Rtm=50G(Open)、寄生容量C0=10pFとしています。また、各伝送路超は50cmとしていますので、全部で2mの長さになります。電圧源V0を信号源として、Voutまでの周波数特性を計算した結果を次に示します。

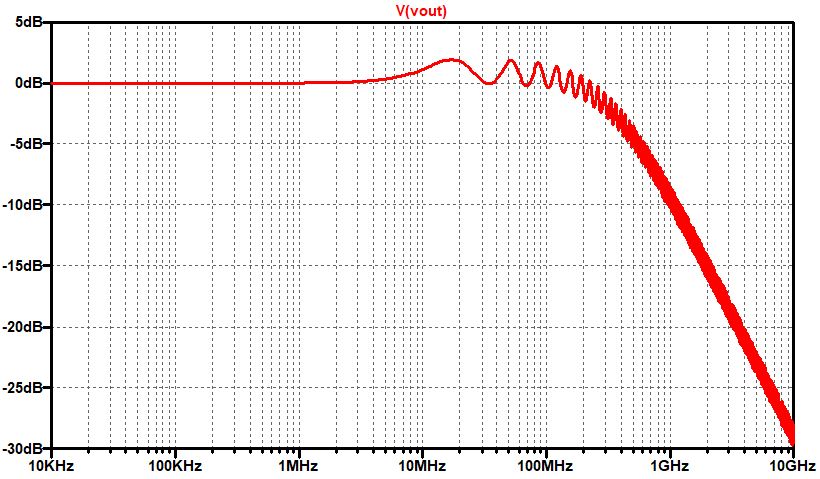
17MHz辺りでピーキングが発生して、それが繰り返されているように見えます。

横軸をリニアに変更した結果を下に示しました。

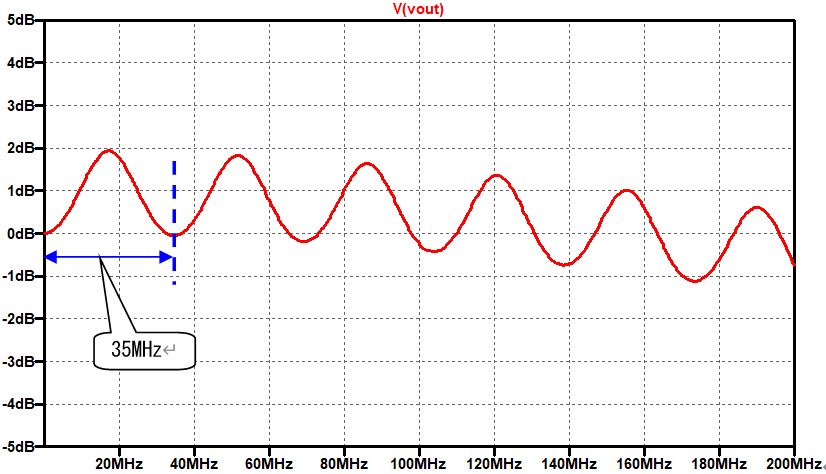
横軸をリニアにすると、同じ形の繰り返しになっていることがよく分かります。周波数は35MHzで形も正弦波のように見えます。

横軸が時間であれば、よくある波形なのですが、このグラフの横軸は周波数です。

周波数特性を知る

あまり見ない形になっているので、これで良いのか少し不安では有りますが、気にせず先に行こうと思います。

先ずは35MHzと言う数字はどこから来ているのか考えてみることにします。 35MHzの一周期は・・・ です。

伝送路の長さは50cm×4＝200cm。伝送路の計算に用いている遅延は70psec/cmとしています（普通のFR-4はこのくらいの遅延になります）。 なので、信号の遅延量は、70ps×200cm=14nsecとなります。14nsecと言うことは の信号ならちょうど一周期分がぴったり伝送路に入ります。

と成ると、 周期では35.7MHzと成り、周期では17.9MHzと成ります。

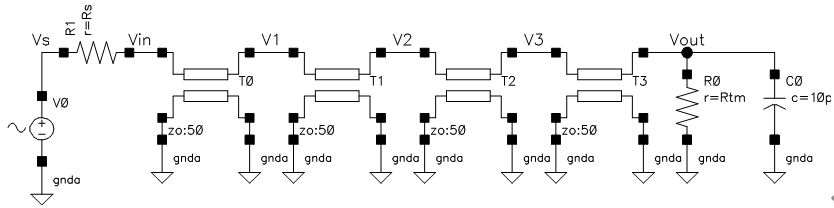
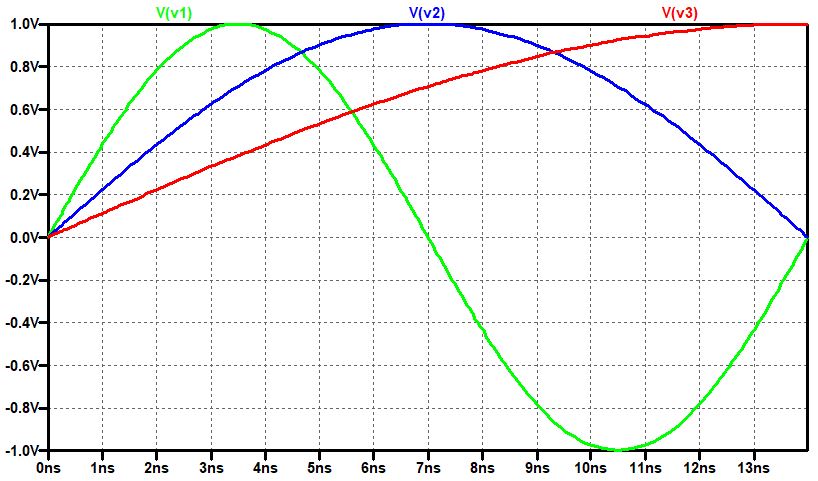
周波数特性でピークと成る周波数は伝送路の中に入れると、“腹”が反対側に表れ、反対に谷となる周波数は、“節”が伝送路の反対側に現れる法則があるようです。 ときどき“反射の影響が出るのはどのくらいの周波数からか？”と聞かれることがあるのですが“伝送路長が 波長になる周波数からかな”と、答えていました。

が図5を見ると、 “伝送路長が 波長になる周波数から。場合に依っては 波長から”と答えないといけなかった事が分かってしまいました（大汗）

例えば、10cmのストリップラインをFR-4基板に引いたときは・・・

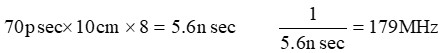
この周波数あたりから利得特性に盛り上がりが現れ、358MHzではピークとなるので、180MHz辺りの周波数では波形に影響が出てくると考えるべきです。

試しに反射を線形解析で解いてみる

ところで、周波数特性が分かっていると言うことは、逆フーリエ変換すれば時間軸波形を求めることが出来るかもしれません。“反射”は周波数特性やフーリエ変換と言った線形解析では解けないというイメージがあるのですが、試してみたいと思います。

入力波形

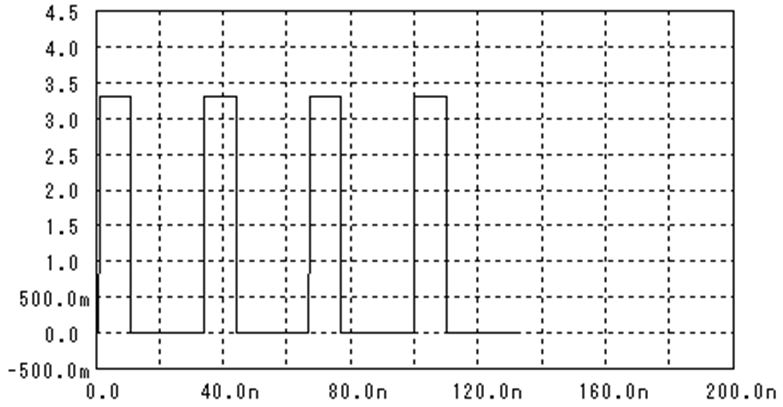
この波形をフーリエ変換すると下記のような周波数成分に分解できます。

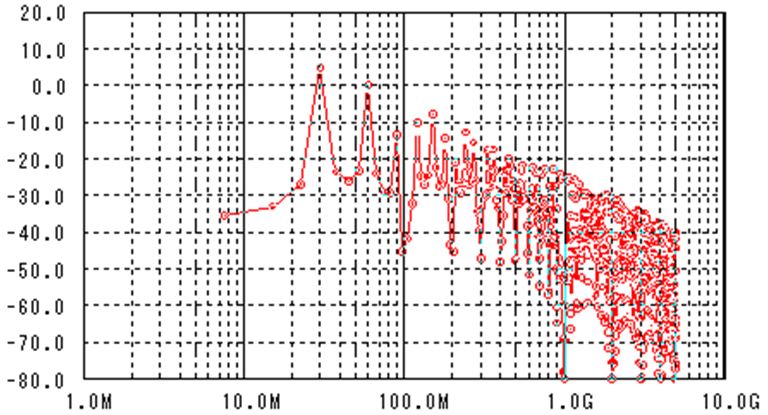
この各周波数成分に下の周波数特性を掛け算して・・・

伝送路の周波数特性

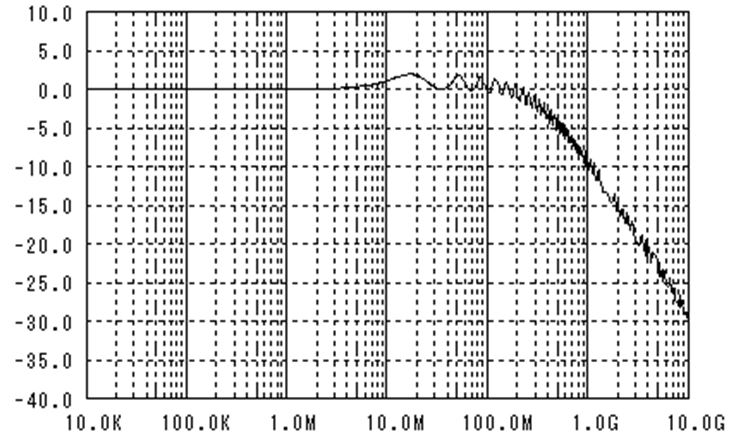
その結果を逆フーリエ変換すると・・・下のような波形になります。

逆フーリエ変換による波形出力

出力波形

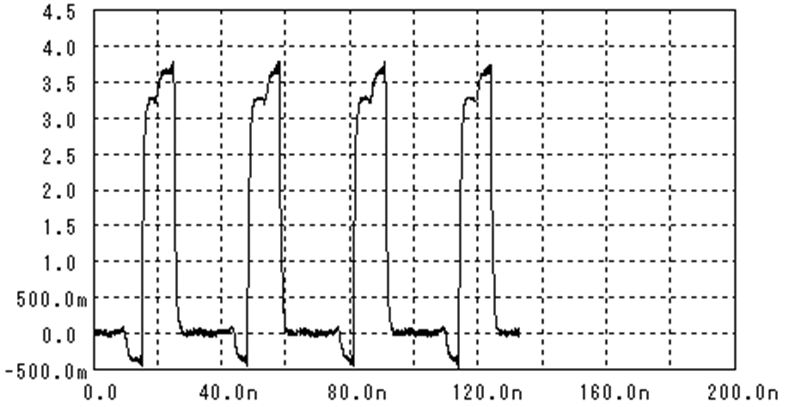
過渡解析と逆フーリエ変換による波形の違い

同じ事を過渡解析で計算してみると、

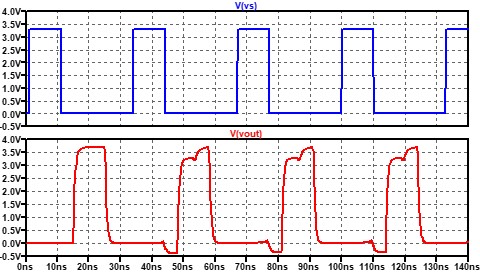
と成って、ほぼ同じ波形を得ることができました。注目すべきは、1個目のパルスです。

周波数特性＋逆フーリエ変換を使った結果では1個目のパルスから歪んでいますが、過渡解析は最初のパルスは歪んでいません。どちらの結果を信じれば良いのでしょうか。

ひずみが発生する原因は多重反射です。パルスが伝送路内に入ってまだ時間が経過してない間は多重反射が起きていない（反射がまだ発生していない）ので、最初のパルスは歪まずに到達できるのです。この辺まで計算してくれる過渡解析の方がより現実に近い計算結果を示していると言えます。

しかし、過渡解析には時間がかかります。伝送路が複雑になると指数関数的に計算時間が増えていきます。反面、周波数特性(AC解析)＋逆フーリエ変換は伝送路の複雑でも殆ど計算時間は変わらないです。最初のパルスを無視すれば、十分使えるのではないかと思います。

今回は“反射”を過渡解析を使わないで計算する方法を紹介しました。

次回は、反射＋線形解析となると避けては通れないSパラメータに触れたいと思います。