今回は「エミッタフォロア（その1-2）」です。

エミッタフォロアがピーキングを出すことを計算で求める

エミッタフォロアは主にバッファとして使う便利な回路ですが、ときどきピーキングを出して（時には発振して）

僕らの頭を悩ませてくれます。特に負荷が容量性(コンデンサがついている)の時は危険度が増します。

前回は、計算の途中までしかできてなかったので、今回はそのやり直しをしたいと思います。

今回は少しモデルを簡単にしました（じゃないと計算力が足りず、解けそうにないです）

エミッタフォロアの周波数特性Simulationを見る

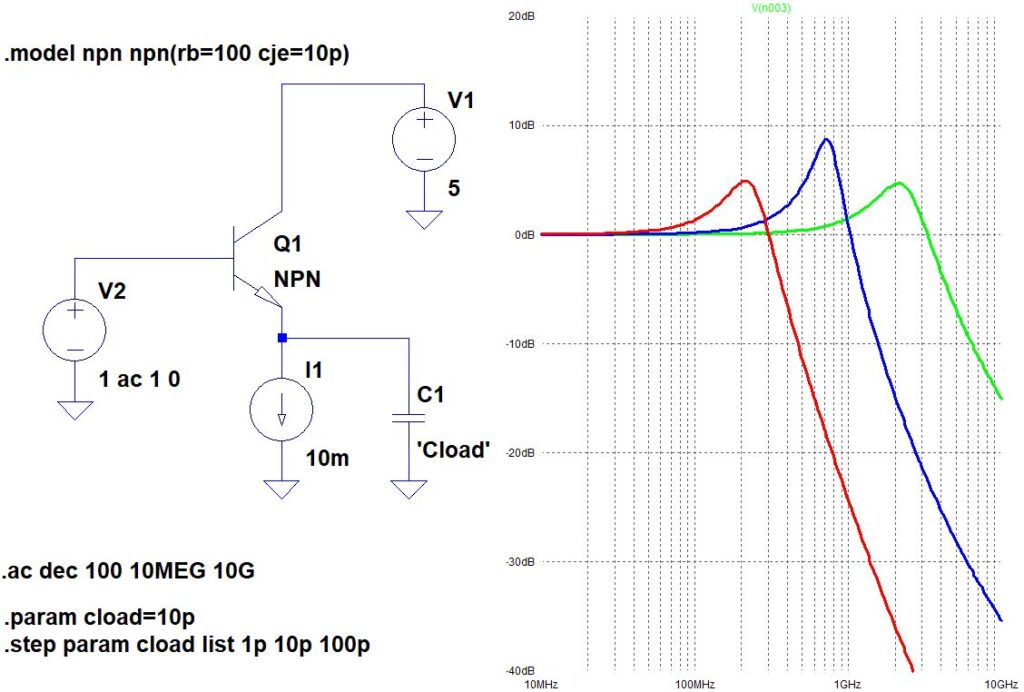
上の図は、エミッタフォロアの周波数特性をSimulationしたものですが、負荷容量を変えるとピーキングが発生します。

等価モデルを使って再説明する

その仕組みについて、等価モデル(下図)を使って説明してみたいと思います。

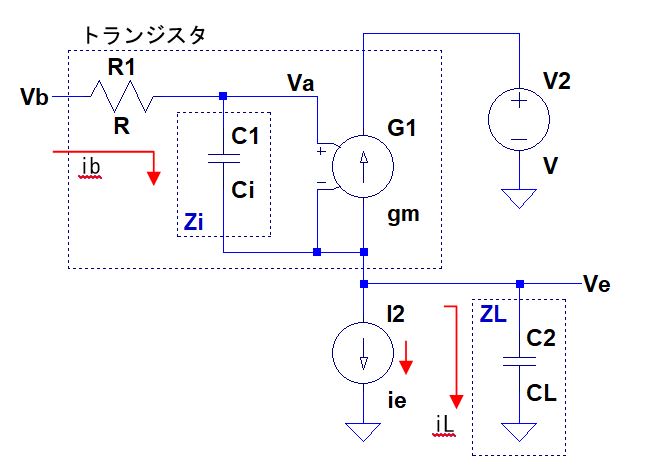
前回よりも楽にエミッタフォロアの関係式を計算で求める

この等価回路から以下の関係式が導き出せます。

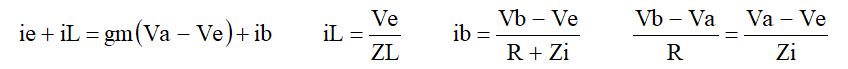
これらを整理して、Veへの伝達関数を求めます。

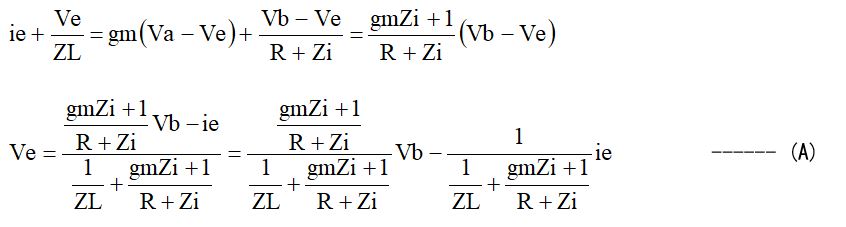
となります。Vb => Veの利得を求めると、

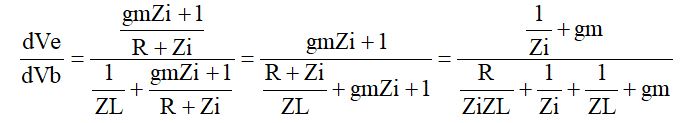
ここで、 を代入すると、

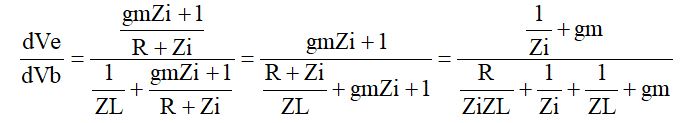
となります（・・・前回よりだいぶ簡単になりました）。

利得の大きさは、

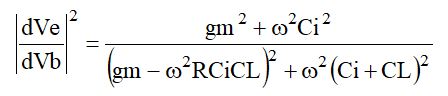
です。

補足：複素関数について

複素関数で、分子と分母の実部と虚部をそれぞれ2乗すると、大きさの2乗になります。

この式で、分母が最も小さくなるのは、なので、このときに利得は、

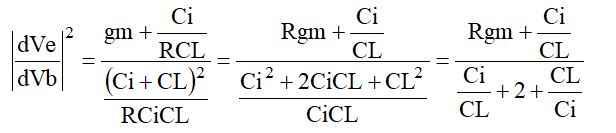
になります。

例えば、CL=Ci=10p、R=100Ω、gm=10mA/26mV=384mSの場合、

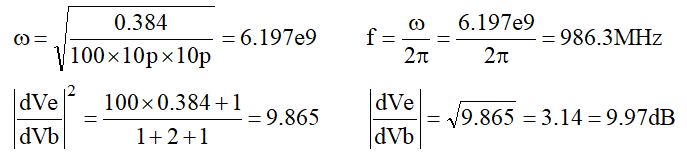
となって、トランジスタを使ったシミュレーションと一致します（・・・よかった(^_^；)

次回は、今回使ったモデルや計算式（A）を使って、エミッタフォロアの入力インピーダンスや出力インピーダンスを計算してみたいと思います。（美斉津）