
FPGAによる、数理最適化における演算スピード高速化の記事2回目です。
今日はマイクロプログラム化とメインプログラム開発についてお話します。前回の記事はこちら。
FPGA内処理概要
簡単な演算(乗算)を例に、今回のマイクロプログラムを動かすFPGA上の回路構成と、そこで実際にどのようにデータが処理されるのかをステップで示しました。
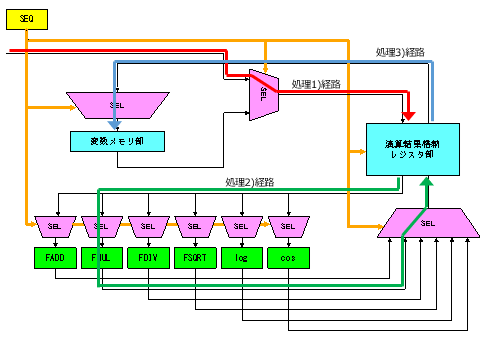
- 処理1(赤色経路): 制御部(SEQ)の命令により、変数メモリ部から演算に必要な変数を抽出し、演算結果格納レジスタ部へ書き込みます。
- 処理2(緑色経路): レジスタ部に保持された変数を乗算器(FMUL)へ投入します。演算された結果は、再びレジスタ部へと書き込まれます。
- 処理3(青色経路): レジスタ部にある計算結果を、変数メモリ部の変数に該当するアドレスへと保存します。
数式(X = A × B)での演算フロー
具体的な処理イメージを持っていただくために、シンプルな乗算の例で追ってみましょう。下図左はA×Bの演算式を処理1~3に分解したもの、右はその処理をマイクロプログラムで記述したものです。
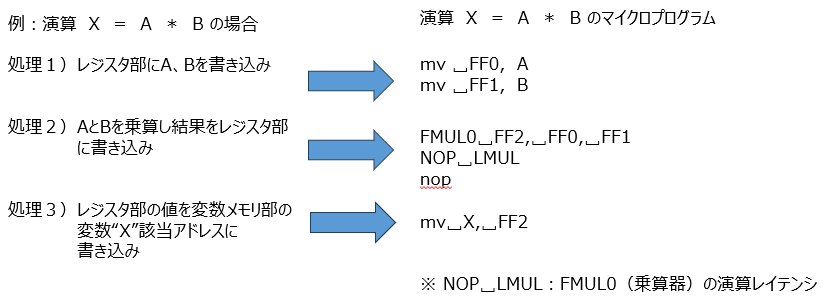
この処理では、処理1) メモリからレジスタへ変数 A, B をロードし(mv命令)、処理2) 乗算器を起動して結果をレジスタに書き込み(FMUL命令)、処理3) 最後にメモリへ書き戻す(mv命令)というステップを順に実行します 。これをマイクロプログラムでは、数式を命令の連なりとして記述しています。
数式のマイクロプログラム化へのステップ
FPGAアクセラレータで扱う数式モデルは非常に複雑なので、これをマイクロプログラムに落とし込んで高速化するために次の処理を行います。
- 数式の分解: 数式を分解して単純計算レベルまで落とし込みます。
- 演算順序のフロー化と共有化: 演算順序(フロー)にしてこれらの計算を共有化。
- マイクロプログラムの記述: 共有化したフローに基づき命令を記述。
- マイクロコード化: ハードウェアが理解できる形式に変換。
分かりやすく説明するため、馴染みのある「2次方程式の解の公式」を例に挙げて解説します。
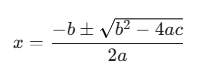
①数式の分解:
複雑な数式をそのまま順番に計算すると、同じ計算を何度も繰り返すことになり、処理時間とリソースの無駄が生じます。そこで数式を分解して単純計算レベルまで落とし込み、各々を回路化します。下図の赤い色の部分が、各々の演算式を分解、単純化した部分です。
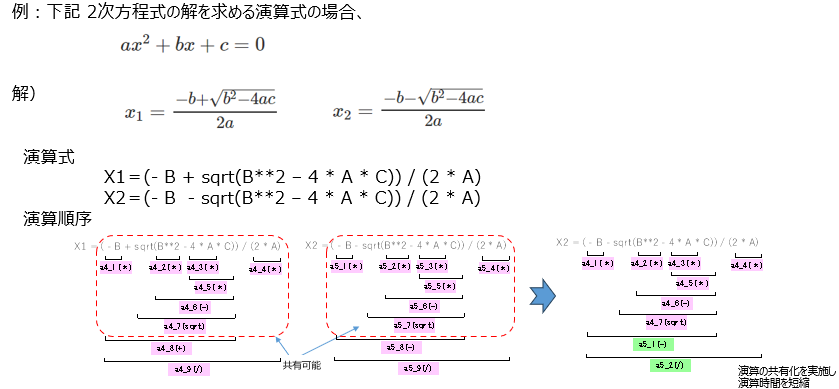
②演算の共有化による重複計算の排除:
上図で2次方程式の解は X1 と X2 の2つがありますが、その中身である![]() や分母の 2a は共通しており、共有化できます。共有化は、演算式の演算順序において、共通する計算ブロック(図中の赤い破線囲み部分)を一度だけ計算し、結果を再利用することで実現します。これにより無駄な演算サイクルを排除し、回路規模を抑えつつ処理時間を大幅に短縮することが可能になります。
や分母の 2a は共通しており、共有化できます。共有化は、演算式の演算順序において、共通する計算ブロック(図中の赤い破線囲み部分)を一度だけ計算し、結果を再利用することで実現します。これにより無駄な演算サイクルを排除し、回路規模を抑えつつ処理時間を大幅に短縮することが可能になります。
③マイクロプログラムの記述
この共有化を想定したマイクロプログラムの記述について少し触れます。図の左側が演算順序(フロー)です。これを、順に右側のように記述します。
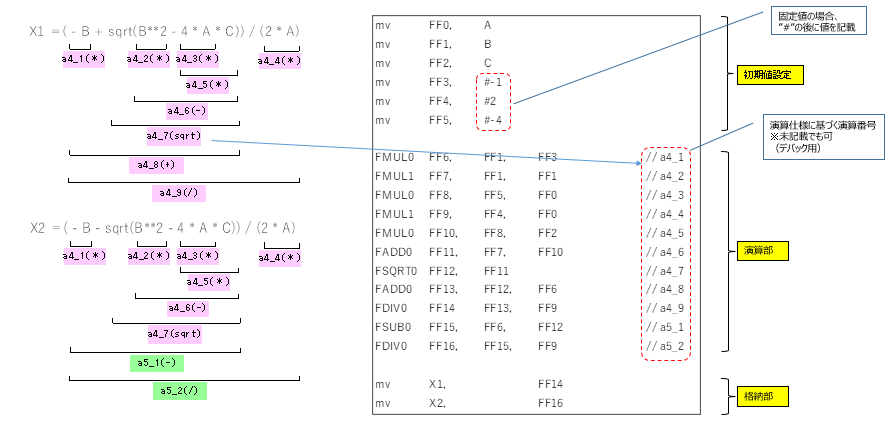
右図のマイクロプログラムはこんな構成になっています。
- 上段)初期値設定:
mv命令で変数 A, B, Cや固定値をレジスタへセットします。 - 中段)演算部:
FMUL(乗算)、FADD(加算)、FSQRT(平方根)などの演算命令を並べ、共有化したフローに沿って実行します。 - 下段)格納部: 最終的な計算結果をメモリへ書き戻します。
共有化した演算パターンの数だけマイクロプログラムを作成し実行させます。
④マイクロプログラムからマイクロコードへの変換
さて次は、記述した「マイクロプログラム」を、ハードウェアが直接理解できる「マイクロコード」へ変換する工程です。
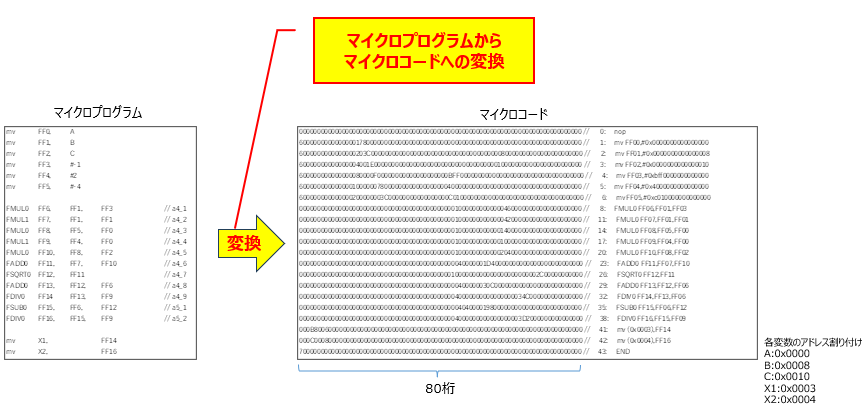
マイクロプログラムは、いわばハードウェア専用のアセンブリ言語のようなものです。設計者が「どのレジスタの値を使い」「どの演算器を起動し」「どこに結果を戻すか」を記述し、それをバイナリ形式のマイクロコード、すなわちFPGA上の演算回路を効率的に叩くための「実行命令の羅列」へと姿を変えます。このように回路を固定せず、マイクロコードを書き換えるだけでハードウェアの演算を変更できる仕組みは、FPGAを用いた高速演算設計の特長の1つです。
単体演算モジュールの開発
いよいよ反応拡散方程式の演算をハードウェア実装していきます。
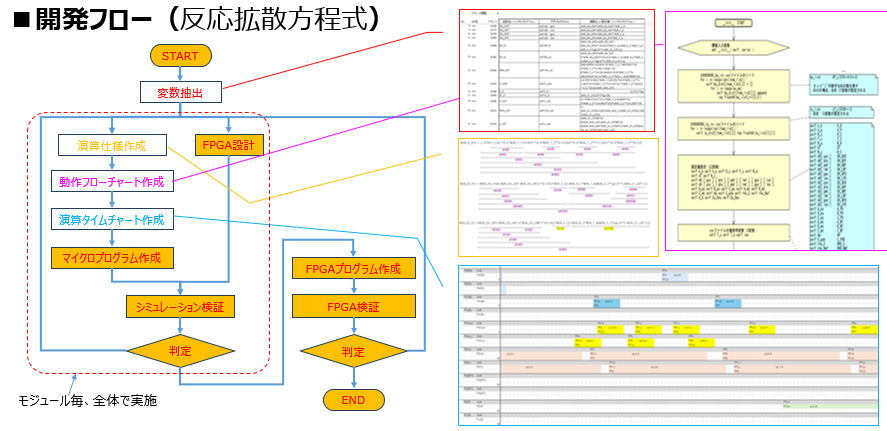
開発のスタートは、Pythonで記述されたソフトウェア演算を「ハードウェアが実行可能な形式」に変換することから始まります。本プロジェクトでは、全体方程式を分解し、その部分部分を担う「単体演算モジュール」を最小単位として設定、開発しました。
ステップ1:演算仕様の策定とマイクロプログラム化
具体的には、Python関数をそのまま移植するのではなく、べき乗や行列演算といった処理を、ハードウェアで実行可能な「単純演算の連なり」へと分解・展開します。この展開された仕様に基づき、マイクロプログラムを作成し、演算タイムチャートを策定することで、演算の順序に合わせてFPGA上でのリソース割り当てタイミングも最適化していきます。
ステップ2:単体演算モジュールのシミュレーション検証
マイクロプログラムが完成した段階で、まずVCSシミュレータを用いた検証を行います。ここでは、展開したマイクロプログラムの演算結果が、元のPythonの期待値と一致することを確認します。この「単体モジュールとしての正当性」をこのフェーズで完全に担保しておくことが、後に続く全体系の構築において、デバッグの迷走を防ぐための極めて重要な関門となります。
メインプログラムの開発:方程式全体の演算を実現する
単体演算モジュールの正当性が確認できたら、次なるステップはこれらを組み合わせて、反応拡散方程式全体の解を導き出す「メインプログラム」の構築です。
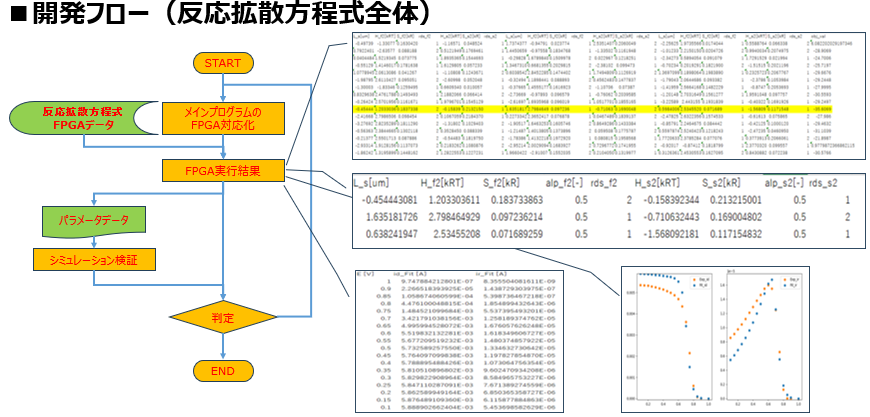
ステップ1:メインプログラムのFPGA対応化
単体モジュールはあくまで計算の一部を担う”部品”です。これを組み合わせて反応拡散方程式の”全体”として機能させるためには、各演算の依存関係を整理し、適切な順序でデータを供給するメインプログラムが必要となります。
このフェーズでは、ソフトウェア側(Python)で管理していたパラメータや計算リソースの受け渡しを、FPGAのアーキテクチャに最適化された形式へと書き換えていきます。
ステップ2:全体系シミュレーションとパラメータ検証
構築された全体プログラムに対し、実際のパラメータデータを投入してシミュレーションを実行します。 ここでは、単一の計算結果だけでなく、時間ステップごとに変化する方程式の挙動が、理論値やソフトウェア実行結果と整合しているかを評価します。
このステップで単体モジュールの集合体が「ひとつの反応拡散方程式」として正しく機能することが証明されたら、実機検証(FPGA実機での動作)へと進むための準備が整います。
今回はここまでとします。次回は演算精度検証とプログラム並列化実装の効果について解説します。