
さて今日は、ΔΣ ADCの2回目です。ΔΣの理論の肝であるオーバーサンプリング、そしてノイズシェーピングのアプローチを、量子化ノイズとの関係を交えながら詳しく解説します。
前回1回目の記事はこちらです。
第2章 オーバーサンプリング
◆オーバーサンプリングとは
オーバーサンプリングとは、信号の帯域幅よりもはるかに高い周波数でサンプリングすることです。
通常のナイキスト系ADCでは、ナイキスト周波数を考慮し、信号帯域の2倍の周波数でサンプリングを行います。
一方、ΔΣADCでは、数十倍から数百倍もの高い周波数でサンプリングを行います。たとえば、10kHz帯域の信号を扱う場合、ΔΣADCでは100倍の1MHzや、1,000倍の10MHzといったクロックで信号をサンプリングします。
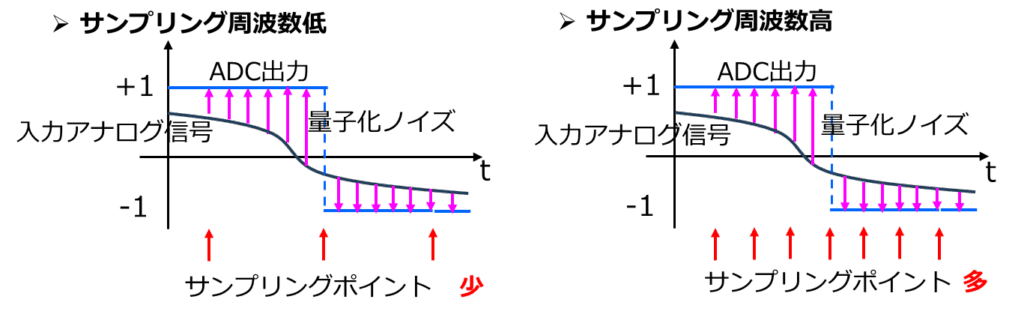
ではなぜ、高い周波数でサンプリングを行うのでしょうか。
・オーバーサンプリングで、ノイズを「薄める」
オーバーサンプリングを行って周波数が変化しても、量子化ノイズの総エネルギーの和は変わるわけではありません。ですからサンプリング周波数が高くなるほど、より広い周波数範囲に量子化ノイズが均等に分布するようになります。つまりノイズが広帯域に拡散し、信号帯域(fs以下)の範囲に含まれるノイズ密度は相対的に小さくなるのです。
これは「ノイズを薄めて信号を取り出しやすくする」と例えれば、わかりやすいかもしれません。
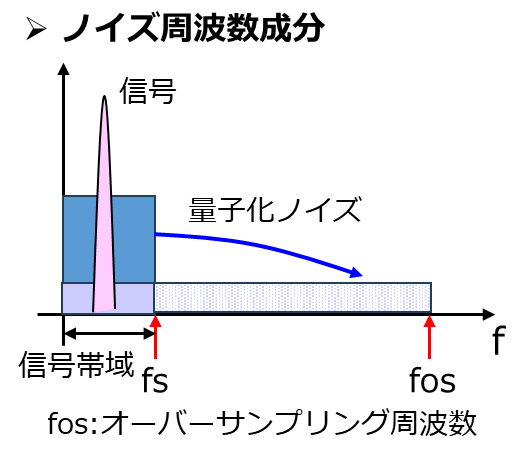
結果的に信号対ノイズ比(S/N比)が向上し、分解能が上がることになります。(但しΔΣADC後段のディジタルフィルタで高域側ノイズをフィルタリングして落とすことが前提です)

・S/N比の改善量(bit数増加)とオーバーサンプリング周波数との関係
オーバーサンプリングによって得られるS/N比の改善量は、サンプリングポイント数に依存します。
おおまかには、オーバーサンプリング周波数を4倍にすると分解能が約1bit向上することが分かっています。2bit増加させたい場合は周波数は4×4=16倍です。ΔΣADCではこれを活用して手っ取り早くbit数増加を実現できます。
(補足)理解を深めるための補足知識
オーバーサンプリングの効果をより深く理解するには、信号処理の基礎となるウィナーヒンチンの定理とパーセバルの等式の考え方が参考になります。
- ウィナーヒンチンの定理:
信号の自己相関関数とそのパワースペクトル密度はフーリエ変換の関係にある。
つまり、ノイズを時間的にランダム化すると、周波数領域では広帯域に分布することを示しています。 - パーセバルの等式:
信号の全エネルギーは、時間領域と周波数領域で等しい。
これにより、「サンプリング周波数を上げてもノイズエネルギーの総量は一定」という考えが導かれます。
この2つの原理は、オーバーサンプリングがノイズの総量を変えずに分布を変えるという考え方を支える理論的背景です。
ココでは詳述は控えますが、詳細な数式を理解しなくても、
「時間を細かく刻むほど、ノイズが平均化されて密度が下がる」と捉えれば十分です。
次回は、量子化ノイズを抑えて信号を取り出すもう一つの重要なアプローチである「ノイズシェーピング」について、フィードバック制御の観点から解説します。
第3章 ノイズシェーピング
次は、S/N比改善のもう一つのアプローチ、ノイズシェーピングについて解説します。
前章で説明したオーバーサンプリングによって、量子化ノイズは広い周波数帯に拡散し、信号帯域内のノイズ密度が下がることを確認しました。
しかし、オーバーサンプリングだけでは、量子化ノイズは帯域全体に一様に分布したままであり、
帯域内のノイズをさらに下げることはできません。
そこで用いられるのが、「ノイズシェーピング(Noise Shaping)」です。
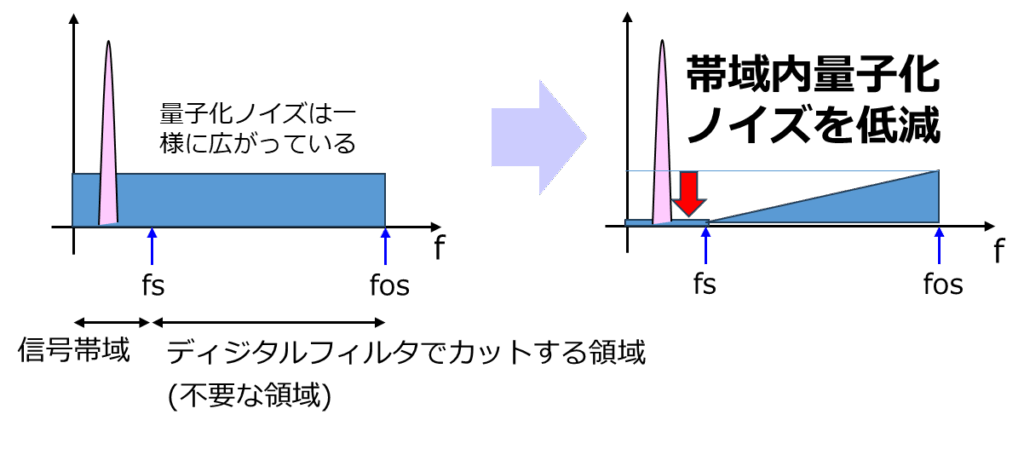
上図の左側は、量子化ノイズが全帯域に均等に広がった状態を表しています。
この状態では、信号帯域(fs以下)にも一定量のノイズが残っています。ノイズシェーピングでは、この信号域内の量子化ノイズをさらに抑圧し、高周波側(fs〜fos付近)へノイズエネルギーを追いやります。
すると、右図に示すように、信号帯域内のノイズが減少します。
このように、ノイズの「量」ではなく「形(周波数分布)」を変えることがノイズシェーピングの目的です。
◆フィードバック制御システムを活用して、ノイズシェーピングを実現
では、どのようにしてこのようなノイズ整形を実現しているのでしょうか。
その鍵となるのが、フィードバック制御システムの原理です。
一般的なフィードバック制御システムでは、入力信号と出力信号の差分(誤差)を取り、その誤差をフィードバックして出力を安定化させます。
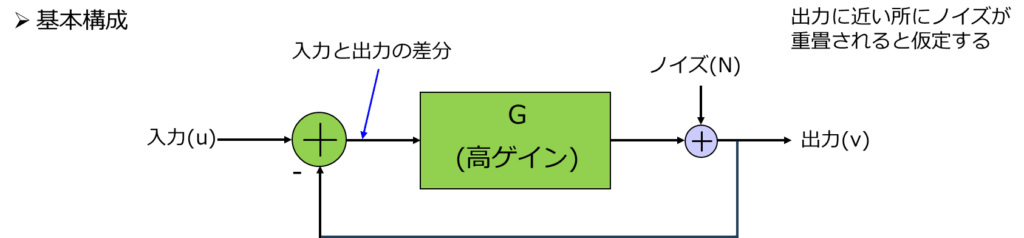
G(ゲイン)が十分に大きい場合、入力信号は正確に出力へ伝達され、一方で、出力側に加わったノイズ(擾乱)は1/G[ゲイン]倍に抑えられます。

この関係は、オペアンプやPLL、DC-DCコンバータなど、多くのアナログ制御回路に共通する基本原理です。
ΔΣADCでは、この制御の仕組みを量子化ノイズの抑圧に応用しています。

量子化ノイズは「出力に付加される擾乱」とみなすことができ、高ゲインな積分器をループ内に配置することで、出力側に生じるノイズ成分をフィードバックで打ち消すことが可能になります。
結果として、信号成分は忠実に通過し、ノイズ成分だけが高周波側へ押し出される――
これがノイズシェーピングの基本動作です。

制御理論の観点で表現すると、ΔΣADCループは「Signal Transfer Function(STF)が入力信号を通過させ、Noise Transfer Function(NTF)が量子化ノイズを抑圧して通さない」という構造になっています。
ループ内のフィルタ(積分器)は低域で大きなゲインを持つため、低域の量子化ノイズは大きく減衰し、結果的に帯域内S/N比が劇的に改善します。
オーバーサンプリングによってノイズを広帯域に拡散し、ノイズシェーピングによって信号帯域内のノイズ成分を制御的に削る――
この二つの効果が重なることで、ΔΣADCは非常に高い分解能を達成しています。ΔΣADCにおけるノイズシェーピングは、フィードバック制御理論をA/D変換に応用した代表例といえます。
この章では、ノイズシェーピングが「量子化ノイズの分布を制御するアプローチ」であり、その実現がフィードバック制御システムに基づいていることを説明しました。次章では、実際のΔΣADCの構成要素――積分器・比較器・ディジタルフィルタなど――を取り上げ、これらのブロックがどのように連携して高精度を実現しているのかを見ていきます。