今回は、交流理論でよく使う“jω(ジェイオメガ)”について話してみたいと思います。
（正式には複素関数っていうのですが、われわれの中ではジェイオメガで通じます）
複素関数
複素関数は、
と書き、jが無いRを実部、jが付いているXを虚部と言います。
この式はZの大きさ
と位相
を表していて、
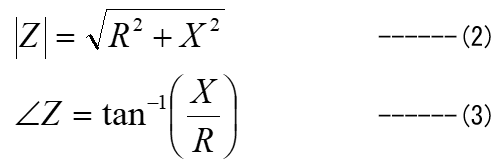
となります。電子回路で扱う要素は”振幅“と”位相“が殆どなので、この(1)～(3)式はオームの法則の次に重要です。なお、電子回路の３要素（抵抗、電圧、電流）は全てこの式で表すことができます。
実際の回路での計算
実際に実部と虚部を計算して見ると以下の様になります。
抵抗器
は、
コンデンサ
は、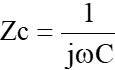
注)ωは周波数をあらわしていて、
です。
インダクタ
は、
です。
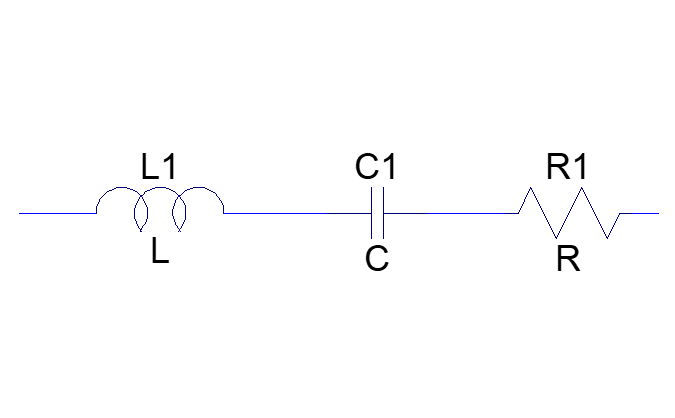
例えば、上の回路の抵抗Zは、
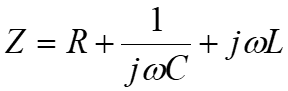
ですが、このままだとjが2個もあって解りづらいので変形すると、
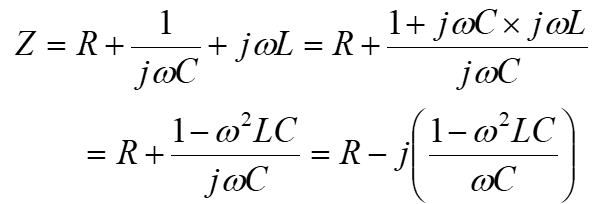
注)j×j=-1なのです。
と成り、実部がRで虚部が
と言う事になります。
これが分かると、この部品をつないだ回路の抵抗の大きさと位相が分かり、
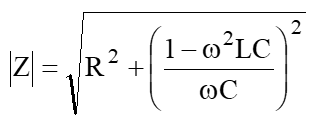
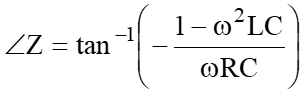
となります。
この式を使って計算すれば、上の回路の細かい特性を求める事が出来るのですが、その計算はエクセルなどにまかせて、先ず僕がすることは・・・
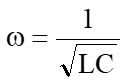
の特性を見ることです。
共振周波数
計算式を見て気づくと思いますが、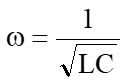は虚部がゼロになるので・・・怪しい周波数です。
一般にこの周波数は共振周波数と言って、この周波数で共振が発生します。
インダクタとコンデンサのインピーダンスが等しくなる周波数なので、お互いに譲らず、共振するわけです。
実際に共振周波数のコンデンサ、インダクタのインピーダンスは、
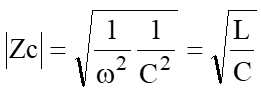
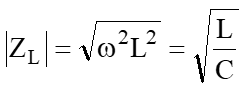
となり、等しくなります。
この2式を知っていれば、ＬＣＲを組合せたたいていの回路の特性を知る（または設定する）ことが出来ます。
共振周波数を知る(又は設定する)には（４）式を、共振の鋭さ(Ｑって言うことが多いです)を知る(又は設定する)には、(5)式と抵抗Ｒに関係を使えば良いのです。
図 1を使って実際に回路に特性を設定して見ましょう。
共振させたい周波数は100KHz、共振時のインピーダンスを1Ωとします。
(4)、(5)式からL=1.6uH C=1.6uF と決まります。
抵抗値はパラメータにしてR=0.1,1,10Ωとした時のインピーダンスをシミュレーションした結果を以下に示します。
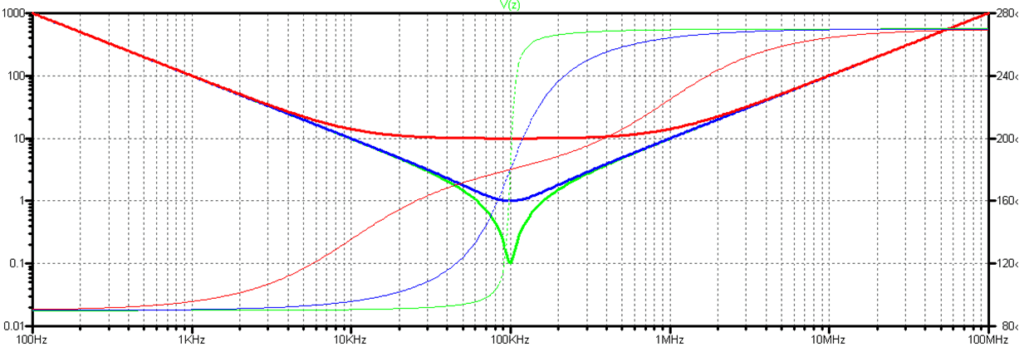
緑：R=0.1Ω、青：R=1Ω、赤：R=10Ωです。
共振の鋭さは抵抗を変更すれば好みに合わすことが出来ます。
この2式を覚えておくと便利
今回は、周波数の計算で良く使う計算式を紹介しました。特に、
の2式を知っていると(オームの法則)、たいていの回路の周波数特性が分かります。
アナログ電子回路の世界は複雑怪奇な事が起きていて理解し難いって思う方も多いと思いますが、実際は、大きさと位相で全てが表現できるので、以外とシンプルな世界なのです。
次はフーリエ変換について書きたいと思います。
