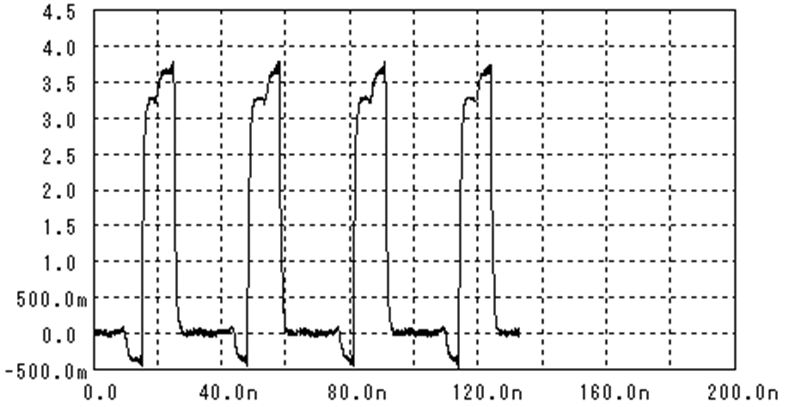
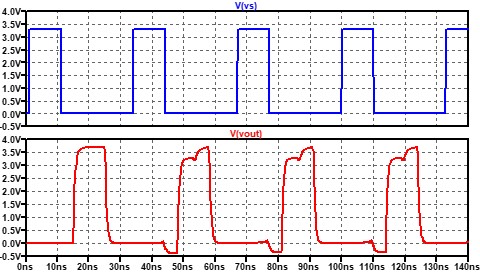
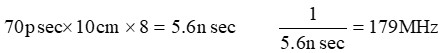高周波の回路設計を行っていると、Sパラメータに必ず出会います。なぜSパラメータと出会わないといけないかと言うと、集中定数では扱えなくなってしまったからです。
Sパラメータ(Sパラ)とは
前回の様に高周波信号は反射を起こします。進行していくものと反射に依って逆方向に進むものとが有り、これらの表現の一つの方法がSパラメータです。
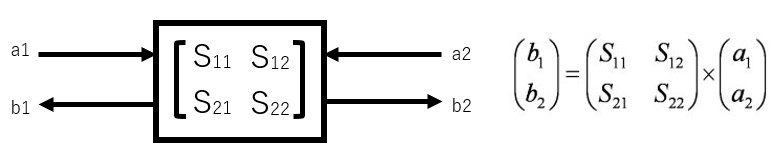
図 1の様に回路網に対して左から入力される信号と出て行く信号、また右側にも入力される信号と出て行く信号が定義されています。つまり、右側も左側も進行波と反射波を考えているという事になります。(注:図でa1とb1は別の端子に見えますが実際は一つの信号線です。入力される信号と出てくる信号を区別するために2本に分かれているだけです)
Sパラとの出会い
私がSパラメータ(以下Sパラ)に出会ったのはHP(Hewlett Packard)のネットワークアナライザーに触ったときでした。高価な測定器だったので、めったに触ることが出来成ったのですが、どうしても満足いく特性が得られず“Sパラを測定してみろ”と先輩に言われて恐る恐る触ったのがきっかけでした。
横軸が周波数になっている測定器との始めての出会いでした。
実はSパラメータは日本人の黒川兼行さんが考案したものであったことをご存知でしょうか?1965年IEEEに発表された“Power Waves and the Scattering Matrix”と言う論文でSパラがこの世に発表されたとのことです。
Sパラとは「散乱行列」
SパラのSはScattering(散乱)からきています。
何が散乱しているのかと言うと・・・Wikipediaに依れば、
「n対の端子を持つ電気回路において、入力方向に進む波の振幅をa1・・・an 、出力方向に進む波の振幅をb1・・・bnとしたとき、次のように記述する。b1 = S11a1 + S12a2 + ・・・ + S1nanb2 = S21a1 + S22a2 + ・・・ + S2nan・・・bn = Sn1a1 + Sn2a2 + ・・・ + Snnan
これらの式を行列を用いて次のように表現する。
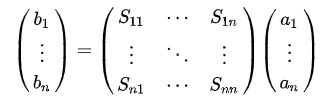
このS11・・・Snnを要素とする行列が散乱行列であり、行列の要素がSパラメータである。Sパラメータの各要素は複素数表現であり、回路の振幅に対する影響に加えて位相に対する影響も内包する。」(引用終わり)
であり、散乱行列と言うのを使うので、Sパラと呼ぶのだと分かります。
正直いうとSパラは私にはまだ分からないことの方が多いです。
SPICEでは電圧や電流を扱うことに慣れているのですが、なかなか電力の方向まで扱うことが少ないため、イメージがつかみにくい事が原因ではないかと思います。
そこでSPICEでSパラを扱うことが出来る回路を紹介したいと思います。
Sパラを回路で理解する
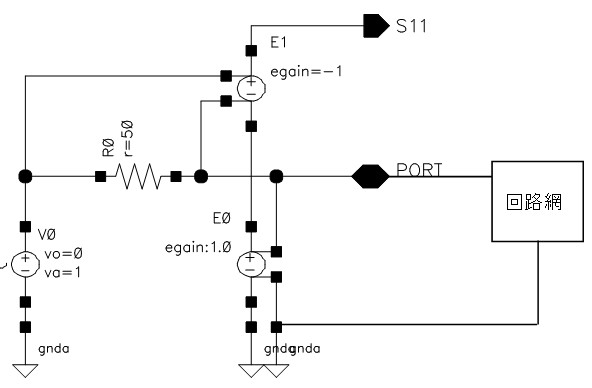
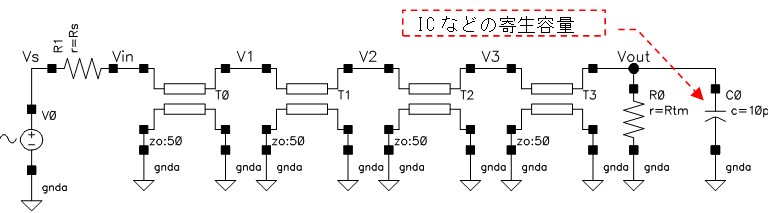
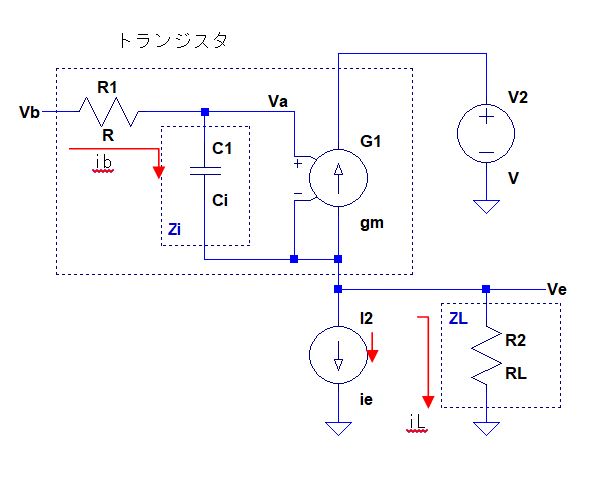
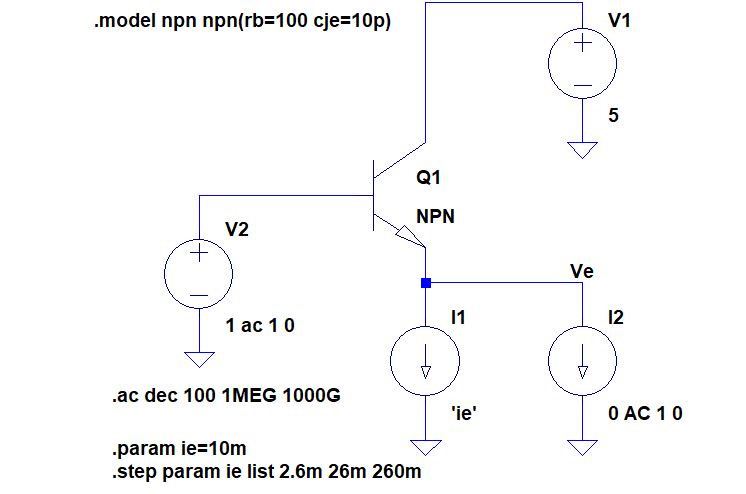
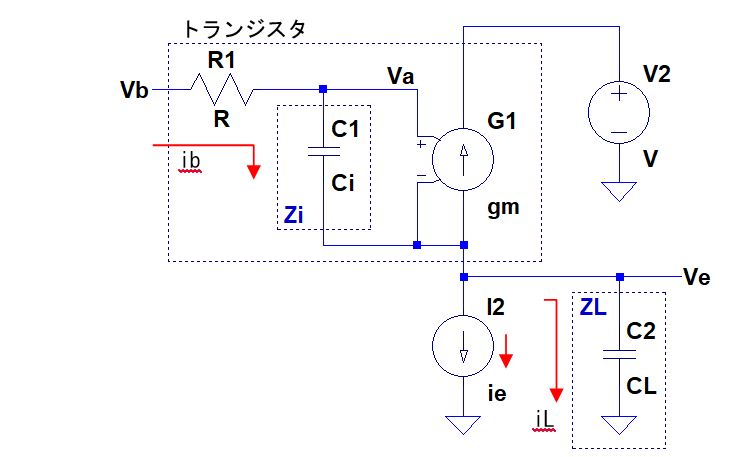
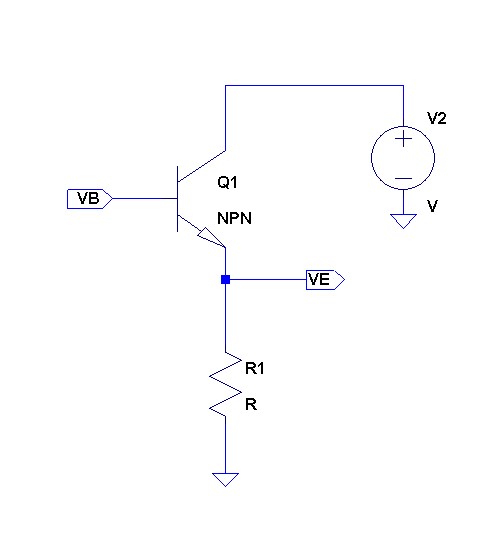
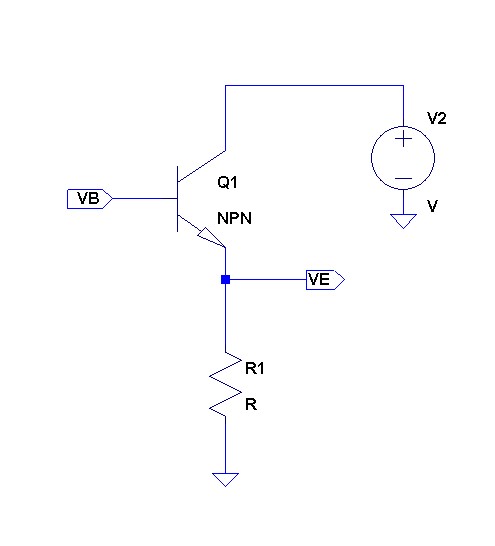
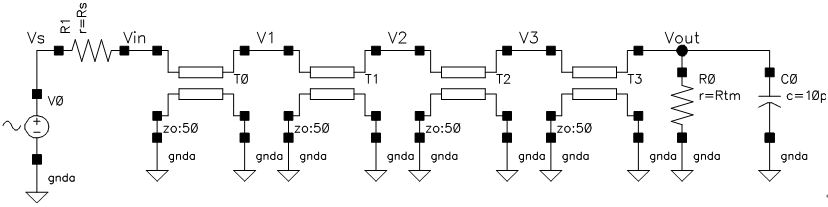
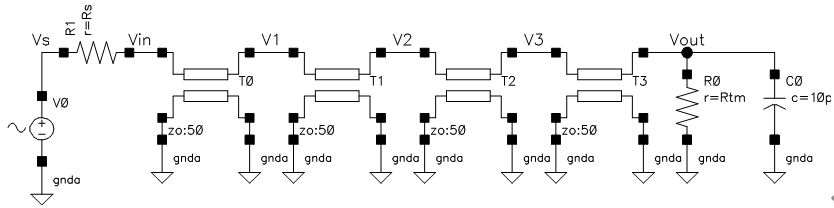
上の回路は端子PORTに接続された回路網のS11を計算して端子S11に出力してくれる回路です。
回路網で発生している電圧(端子PORTの電圧)を依存電源E0で検出し、信号源インピーダンスR0で発生している電圧を依存電源E1で検出して、前者の電圧から引いているだけです。
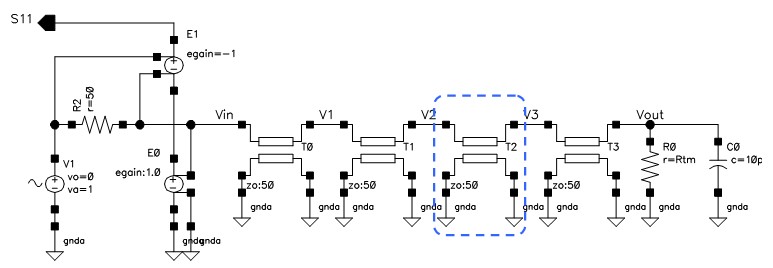
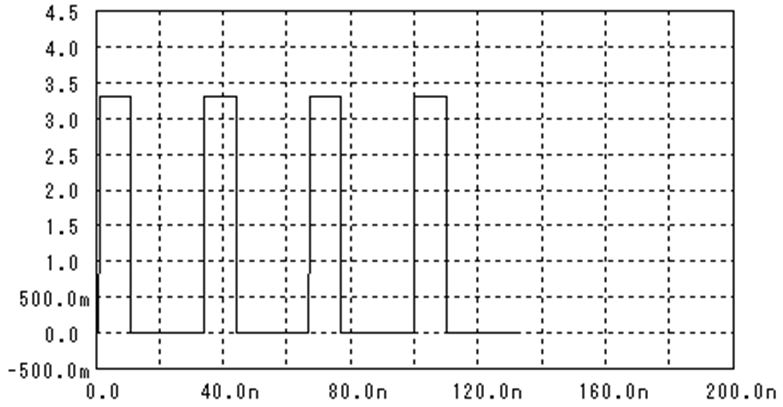
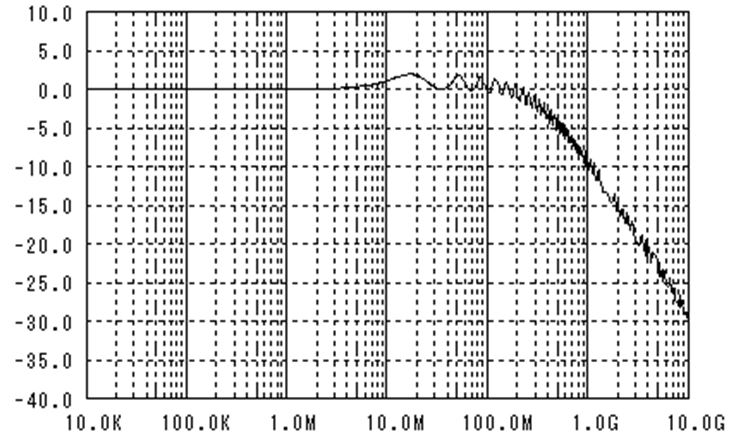
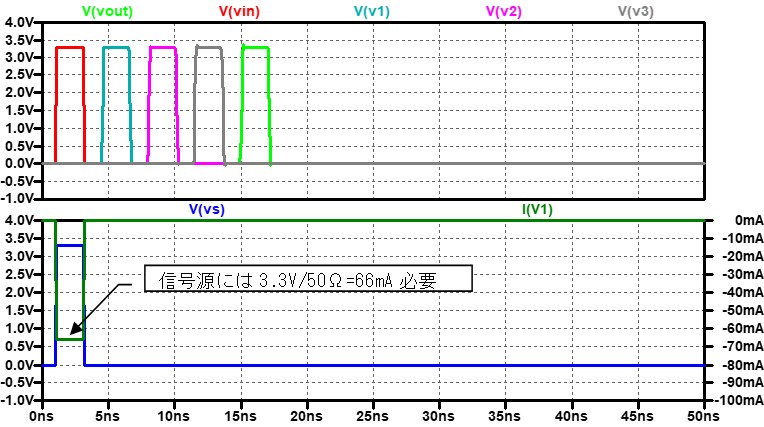
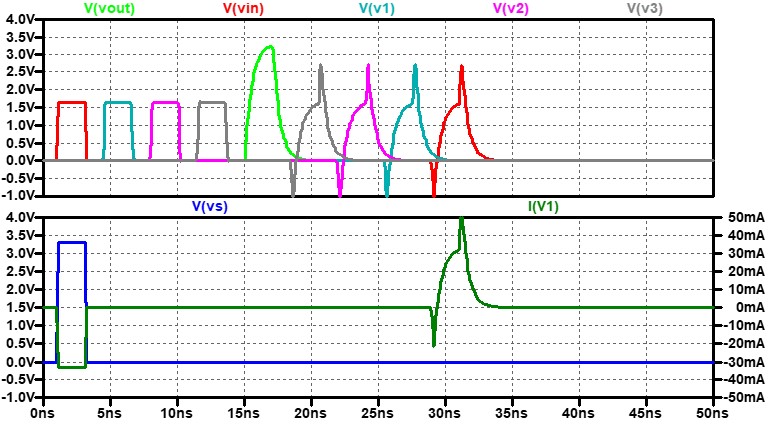
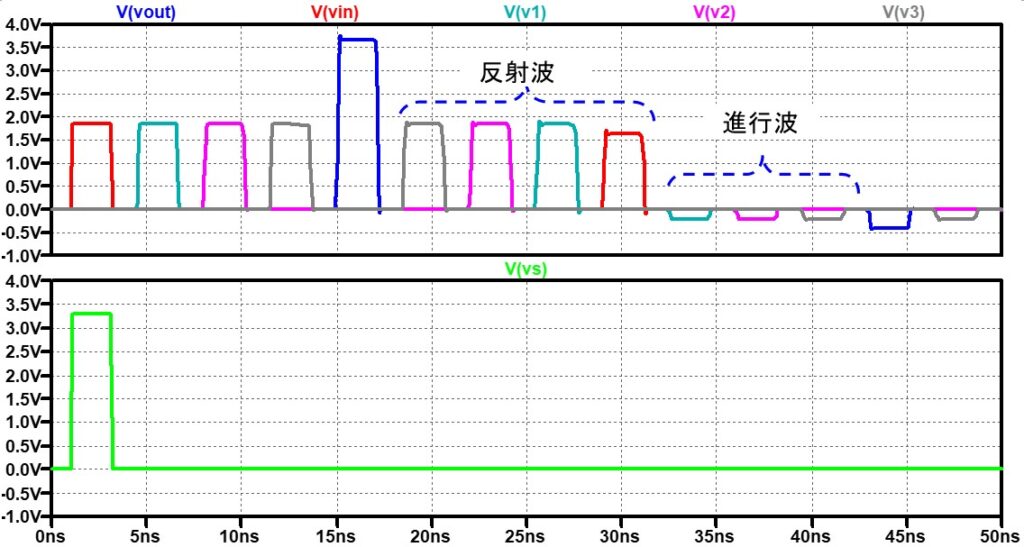
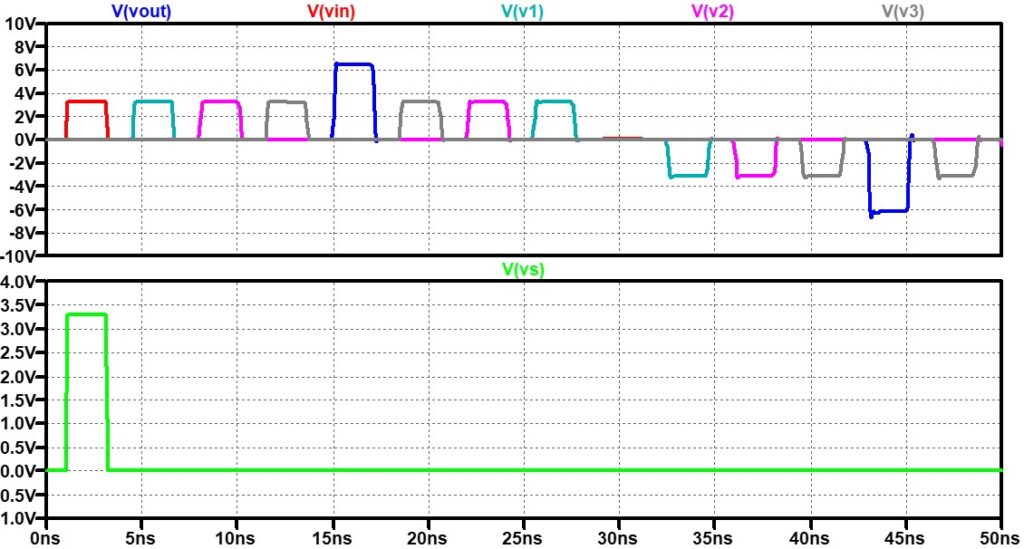
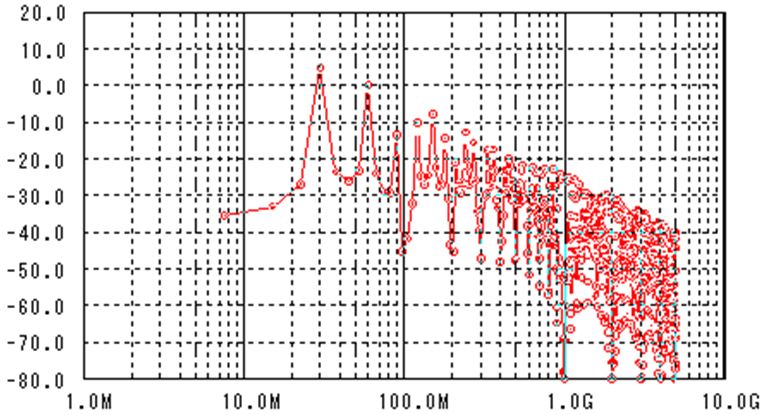
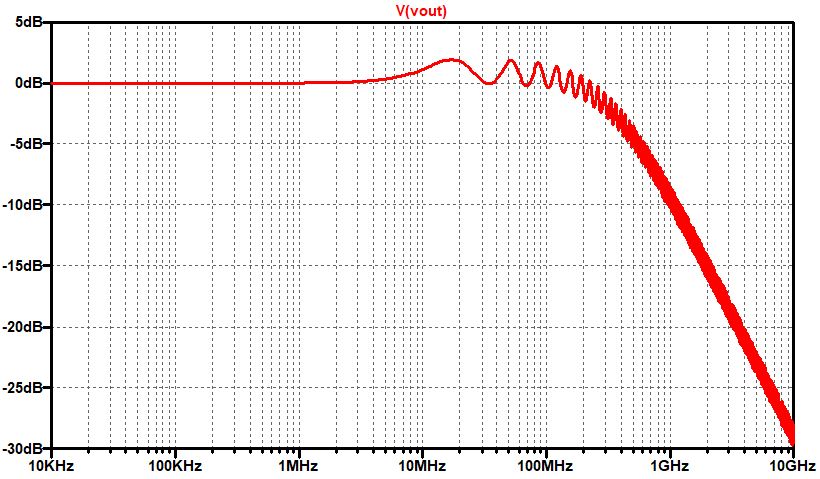
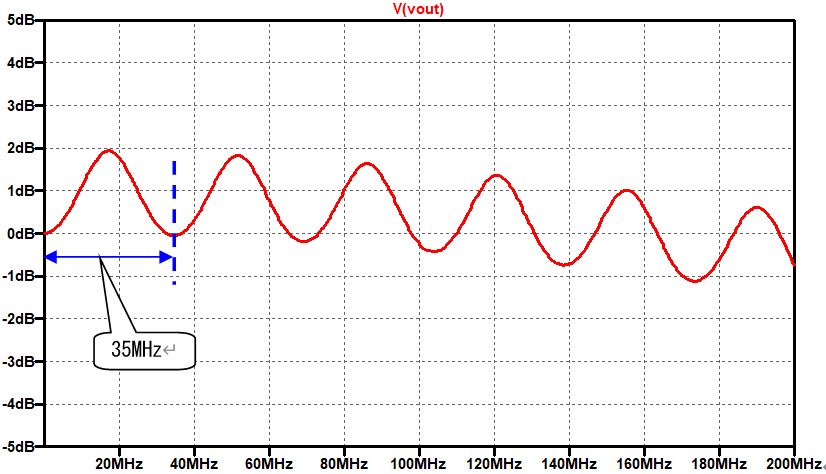
今まで使っていた伝送路のS11を計算してみましょう。終端抵抗の値Rtmは50Ωです。
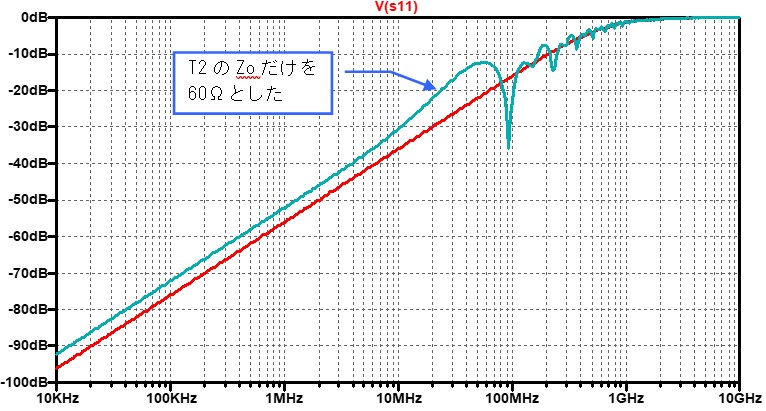
低周波ではS11は低い値を保っています(つまり、反射が少ない)が、高周波に成ると
終端抵抗と並列に入っているコンデンサC0(10pF)の影響でS11が増加します。
図 1から
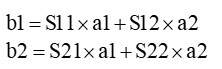
と表されます。もし、a2=0ならば(つまり、回路網の右側から電力が入力されない時)
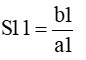 となって、反射係数と同じ計算式となります。つまり、
となって、反射係数と同じ計算式となります。つまり、
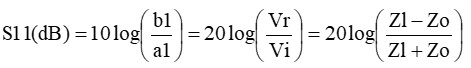
と書くことが出来て、S11が分かれば回路網のインピーダンスZlがわかる事に成ります。
例えば200MHzのZlは終端抵抗Rtm=50Ωと10pFとの並列なので、
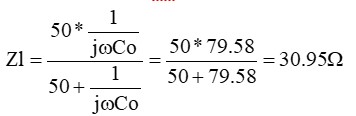
に成っているのでS11は、
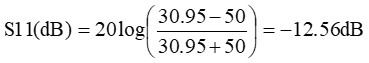
となり、シミュレーションがほぼ正しいことが分かります。
非常に興味深いSパラの世界
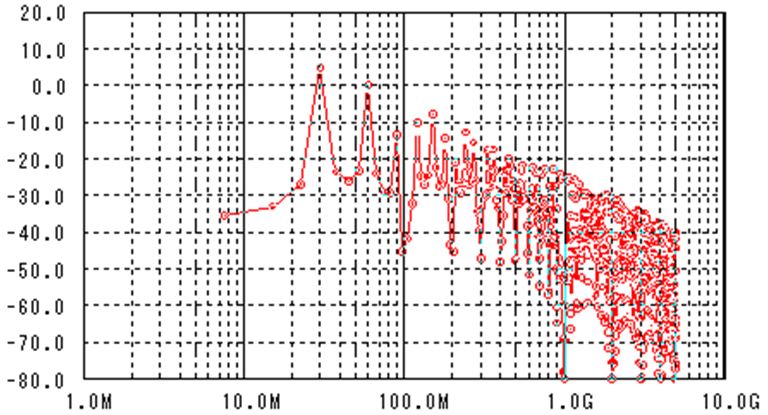
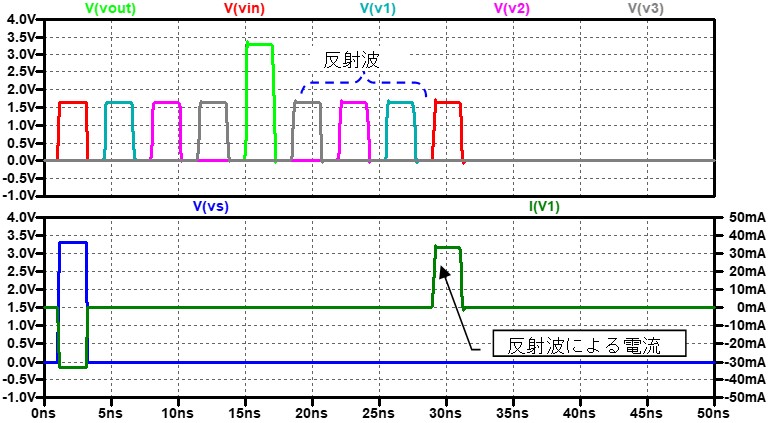
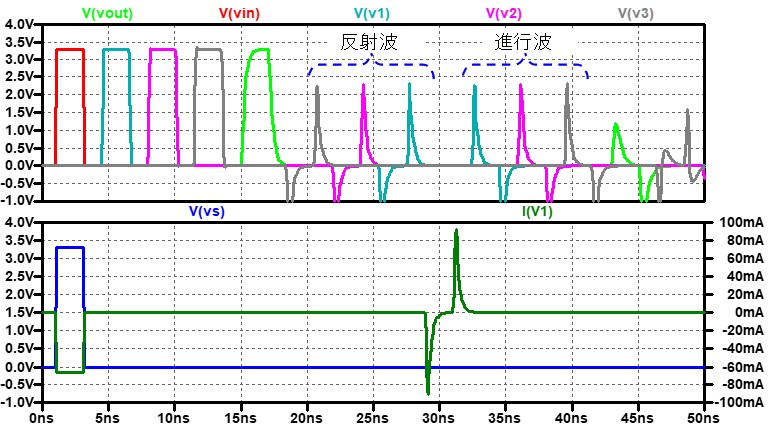
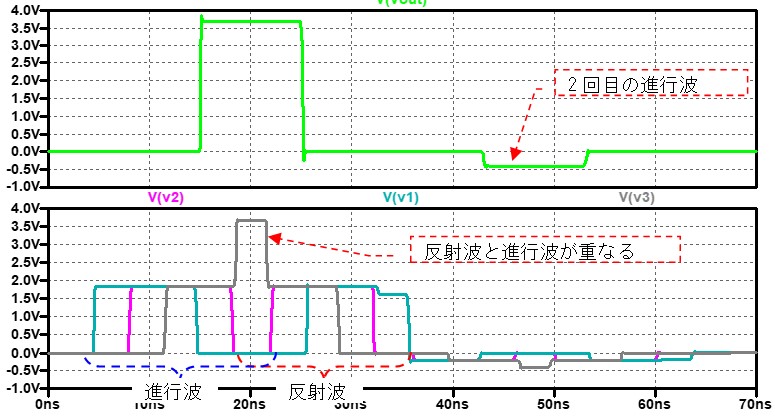
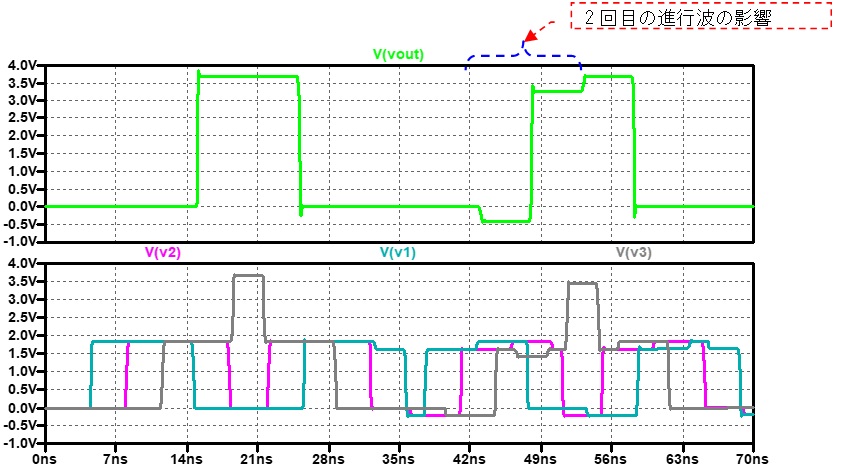
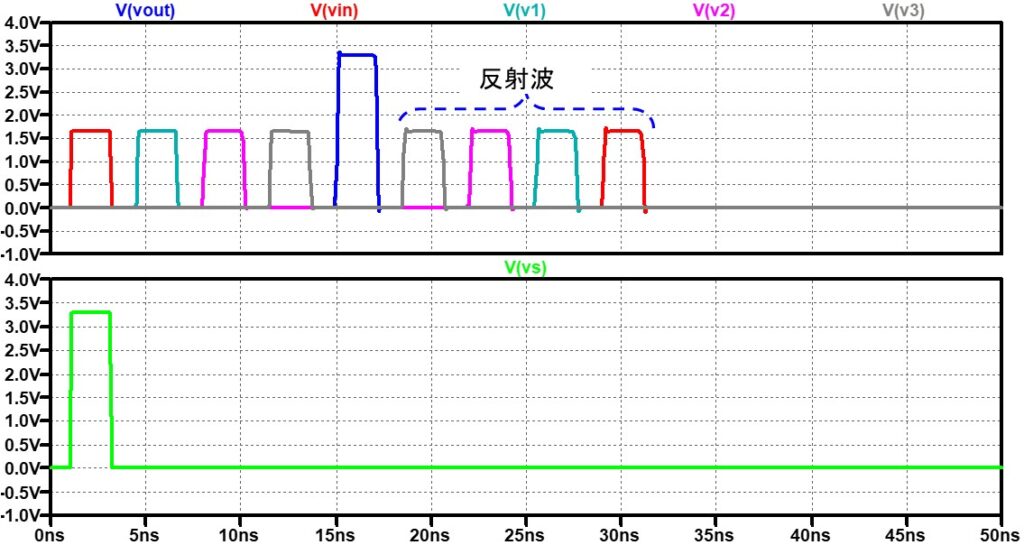
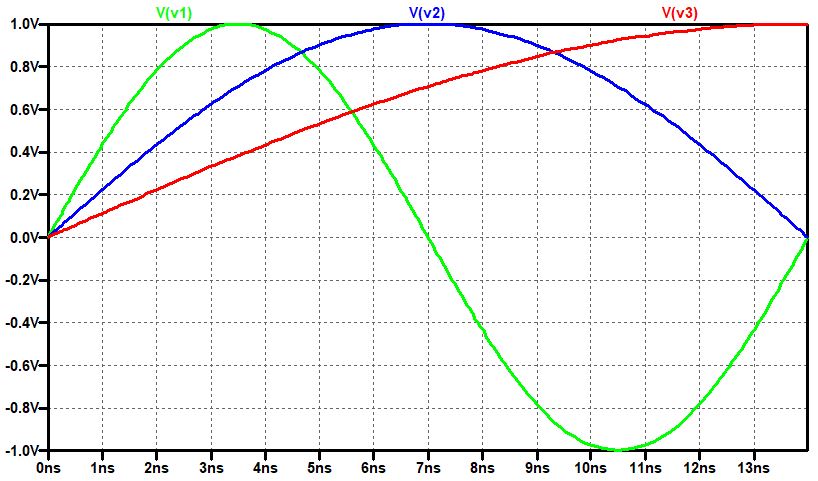
伝送路の右から2つ目の特性インピーダンスZoを意図的に(製造誤差等を想定)60Ωにした結果も図 5にプロットしました。
この結果がネットワークアナライザーの実測とどのくらいの精度で一致しているかの確認はできないですが、大きなずれはないように思います。
高周波の世界でも、相手に伝えたいことがほんとに伝わるのには時間がかかることや、今までの環境と異なる環境にはスムーズに入っていけない事など、人の社会と同じようなことが起きているのが非常に興味深いです。
次回もこのSパラの世界を紹介する予定です。
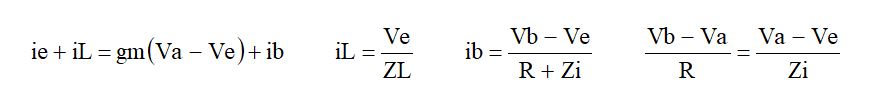
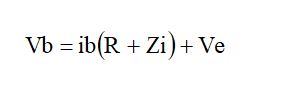
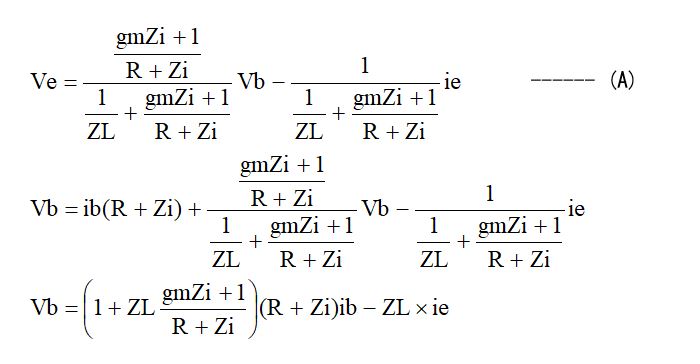
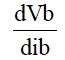
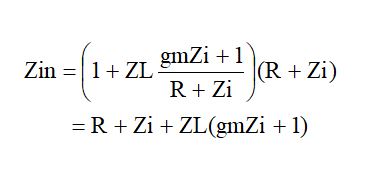
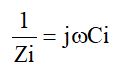
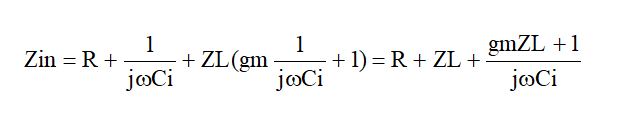
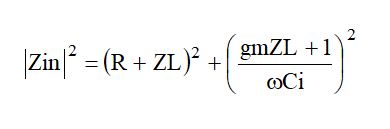
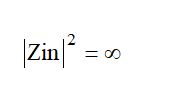
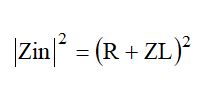

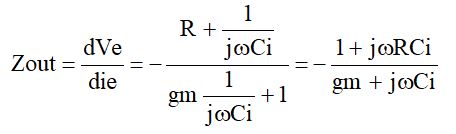
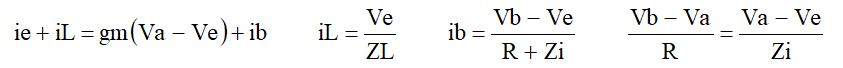
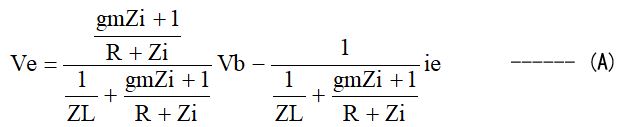
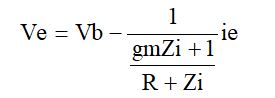
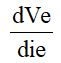 を求めればよいことになります。つまり
を求めればよいことになります。つまり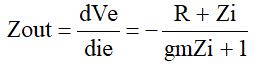
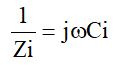 を代入すると、
を代入すると、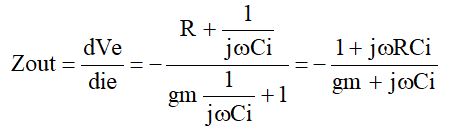
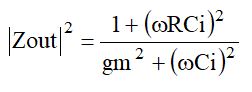
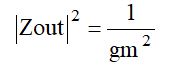
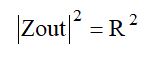
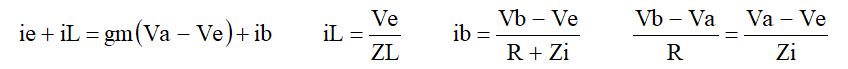
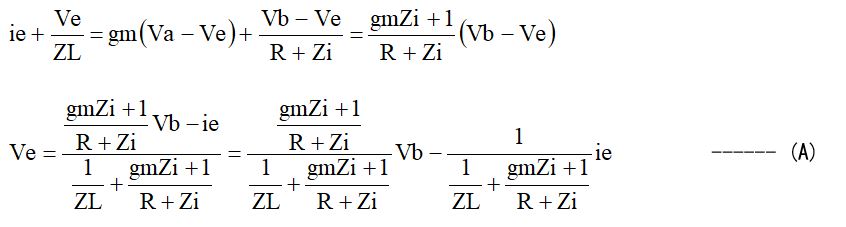
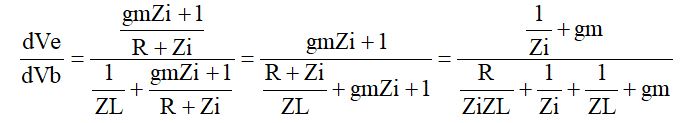
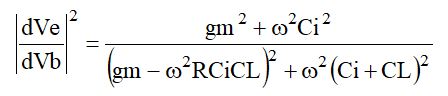
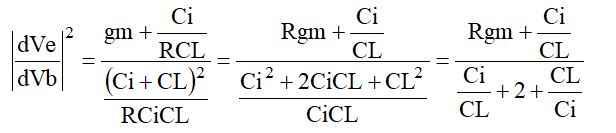
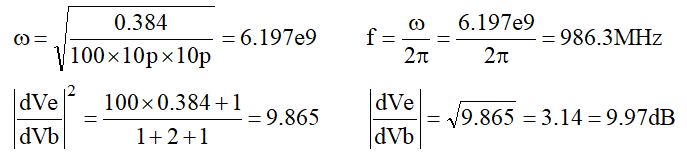

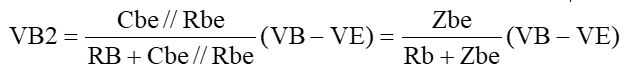
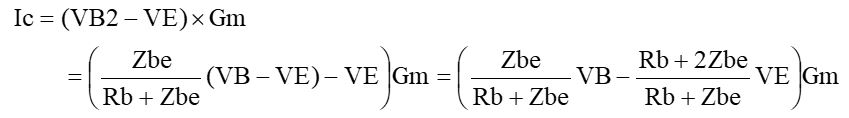
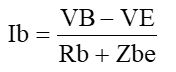
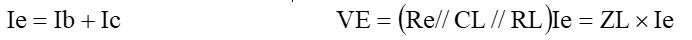
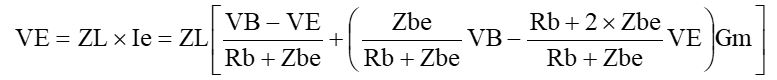

 です。
です。

 波長になる周波数からかな”と、答えていました。
波長になる周波数からかな”と、答えていました。 波長になる周波数から。場合に依っては
波長になる周波数から。場合に依っては 波長から”と答えないといけなかった事が分かってしまいました(大汗)
波長から”と答えないといけなかった事が分かってしまいました(大汗)