
こんにちは。今、日本のアスリートが国際舞台で躍動していますね。彼らアスリートのフィジカルサポートには可搬式の超音波診断装置が用いられていて、チームドクターが練習場等に診断装置を持ち込み、筋肉やじん帯などを可視化して、治療方針の策定に役立てているそうです。これら診断装置には信号処理技術が使われていますので、わが社の信号処理技術がもしやメダル獲得につながっているかもしれない!などと勝手な想像をしてしまいます笑
さて、これまでの記事でご紹介した、ディジタル信号処理の周波数成分の求め方のおさらいです。
離散フーリエ変換のおさらい
- 正弦波の周波数を少しずつずらして内積を求めれば、全周波数成分が求められる。
- ただし、cosとsinの内積は0(相関なし)になるので、cosと分析対象の内積、sinと分析対象の内積、それぞれの値を求める必要がある。
- cosとsinそれぞれの内積で求めた値が、各周波数成分の大きさである。
ここまでがご理解いただければ離散フーリエ変換の本質はばっちりです。
いままでの記事での内積計算を実践してお分かりいただけたと思うのですが、cosとsinの内積をそれぞれ求めて合計するのは、いかんせん手間がかかります。なので、これをシンプルにする計算テクニックをお伝えします。まず離散フーリエ変換の計算テクニックとして必要な部分を中心に、オイラーの公式、虚数、複素数についてそれぞれ触れ、最後に公式を用いた計算の実践までお伝えいたします。
計算テクニックのポイント
離散フーリエ変換の計算テクニックのポイントは以下の4つです。
- オイラーの公式の活用
- 複素正弦波を導く
- 複素正弦波の回転を視覚的に示す
- 複素正弦波の内積を求める
オイラーの公式の活用
オイラーの公式は、フーリエ変換の計算テクニックにとって強力なツールです。世代によって高校カリキュラムではやっていないそうで、私の時代も範囲外でしたが、次の世代のカリキュラム改革で範囲内になったと聞いたことがあります。
公式は以下のように表されます。
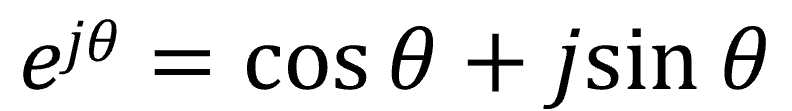
eはネイピア数という定数です(詳しい説明はここでは割愛します)。θは実数(xと記述することもあります)です。オイラーの公式を使うと、右辺のcosとsinの2つの三角関数を、左辺の指数関数1つですっきり表すことができます。虚数jがあるので複素数の理解が多少は必要になりますが、それ以上に式をシンプルにしてくれるメリットがあります。
複素正弦波を導く
まず、オイラーの公式を利用しながら、周期的な波を回転で示す指数関数を導きます。
周波数fとは1秒間にf回同じことを繰り返す周期的な波のことですが、まずこの波を回転で示します。 1秒間に一回グルっと回すとは、360°/1秒=2×180°/1秒=2πfです。(角周波数といいます)
これをオイラーの公式に代入しますと、こうなります。
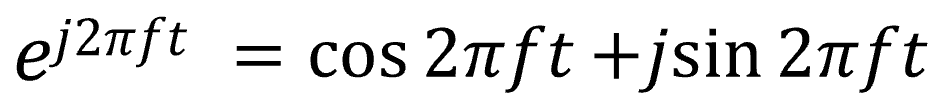
このときの左辺![]() を、周期的な波を回転で示す指数関数、複素正弦波と呼びます。
を、周期的な波を回転で示す指数関数、複素正弦波と呼びます。
複素平面で複素正弦波の回転を示す
次に、この複素正弦波の回転を視覚的イメージするために、縦軸を虚数軸j、横軸を実数軸tとする特殊な平面をご用意しました。これは虚数と実数で成り立つ複素数を理解しやすくするために作られた表現で複素平面と呼びます。
ここに複素正弦波を表すと、図1の感じになります。これを見るとお分かりのように、複素正弦波は複素平面上で、0を中心にして2πftの増加に伴い、
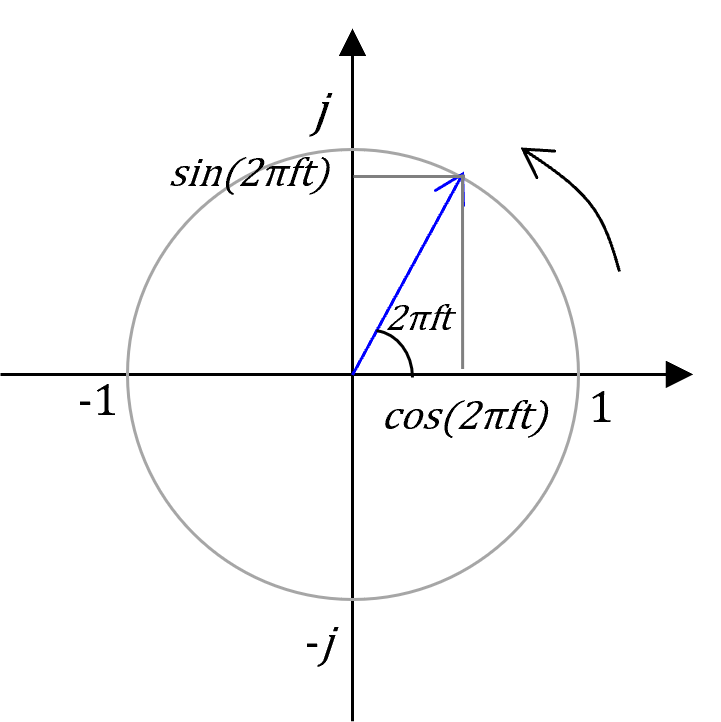
複素平面上の円周をぐるぐると回る周期関数となります。2πftのfの値を増やせば、同じtの変化量(Δt)に対してより大きく回転しますので、周期関数の回転速度もより速く(周波数がより高く)なります。複素正弦波は、指数に虚数がついているため取っつきにくい印象の式ですが、このように複素平面上でぐるぐる回る図にすると理解しやすく感じられたらうれしいです。
いかがでしたか? 次回は今日の基本情報踏まえ、離散フーリエ変換の公式で複素正弦波との内積を計算していきます。
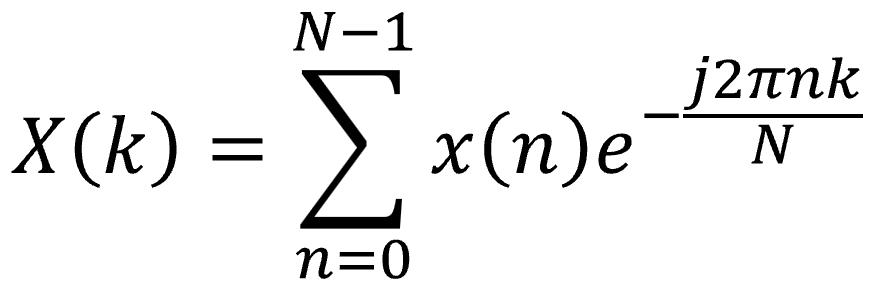
コメント
この記事へのコメントの受付は締め切りました。