
こんにちは。
さて、前回は入力信号の周波数を少しずつずらして正弦波との内積を求めれば、あらゆる周波数成分の大きさを成分検出できそうということでした。前回記事はこちらです。
では検証してみましょう。
ずらした入力信号の周波数成分を求める
まず、2つの入力信号を時間で少しずらします。それぞれ、
・入力信号① 周波数1Hz(振幅1) :0 秒のとき 値1 → 値0 これを①´とする
・入力信号② 周波数2Hz(振幅0.5):0 秒のとき 値0.5 → 値0 これを②´とする
それぞれ、図1ような波形に変わります。少し時間だけずらしただけなのですが、波形にするとずいぶんと違いますね。
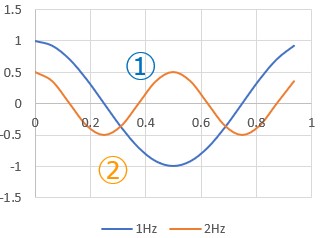
→
図1
なお、検出用の正弦波は前回と同じ ④cos(2Hz)です。
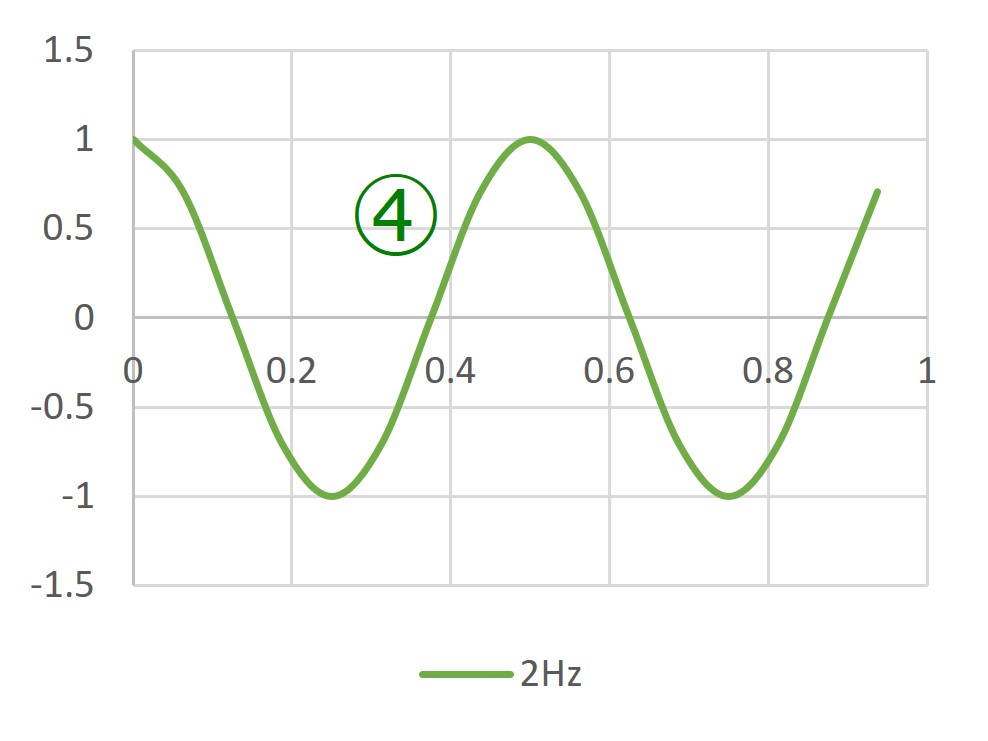
ずらした信号とcosとの内積が0?
これら3つの波形を、前回同様、内積を求める時間単位の一覧表に展開して、内積を計算してみましょう。入力信号①´とcos③、入力信号①´とcos③を時間毎に掛け算していき、最後にそれらの和を求めるのでしたね。さて結果はどうなったでしょうか。
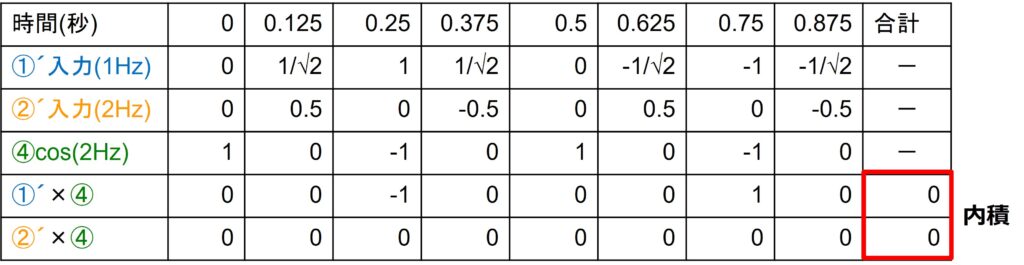
おや? 内積が0になってしまいました。。。
周波数の違う①´はさておき、②´の2Hzの成分は一体どこに消えてしまったのでしょうか?
考察:内積が0になった理由を考えてみる
もちろん、2Hzの信号自体が消えてしまったわけではありません。
実は2Hzの信号②´はずらした結果、sin波になっています。そして重要なのがsinとcosの関数同士の内積は0(相関なし)になるという性質です。専門的には「関数の直交性」といいます。(イメージ的には直交するベクトル同士の内積が0になる「ベクトルの直交性」と非常によく似ています。あくまでイメージですが)
数式で証明しましょう。高校数学でも出てきた、sinとcosの積とsinの2倍角の公式で考えます。
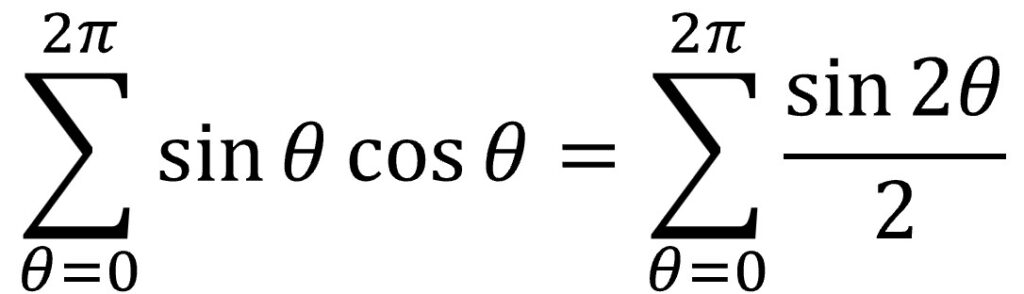
左辺はsinとcosの内積です。sinΘとcosΘの積を全ての角度(0から2πの2周期分)にわたって合計することを意味します。それを2倍角の公式で変形しますとsin2Θ(正弦波sinの2周期分)の総和となります。右辺の正弦波2周期分のsin2Θの総和は、これ実際に計算すると0になりますので、右辺が0となり、左辺のsinΘcosΘの積の和である内積は、0(相関なし)になります。
関数の直交性は何を意味するの?
関数の内積が0=関数の直交性と、sin2Hzが検出できない問題がどうつながるの?という声がでそうですね。ここでお伝えしたかったのは、cosで成分検出できない波は、sinとの内積で検出が出来るということです。

色のディジタル表現をイメージすると案外わかりやすいかもしれません。カラーディスプレイでRGB方式がありますが、赤R緑G青Bの基本3色を256段階で配分してさまざまな色を表現できますね。信号処理では、直交性を持ち、性質が異なるsinとcosの関数2つでさまざまな信号成分が表現可能なんです。
また色で信号処理をたとえてしまいましたが(笑)、すべての波がsinとcosのたった2つの組み合わせで表現可能ということ。あらためてこのシンプルさが私はすごいなと思います。
cosでは検出できない周波数成分をsinで求める
ではsinとの内積であれば先ほどの信号が検出可能か念のためやってみましょう。入力信号①´②´の2つの信号と、sinとの内積を求めてみます。検出用に④´sin(2Hz)を用意し、周波数成分を求めてみます。
内積を求めてみると、このようになります。
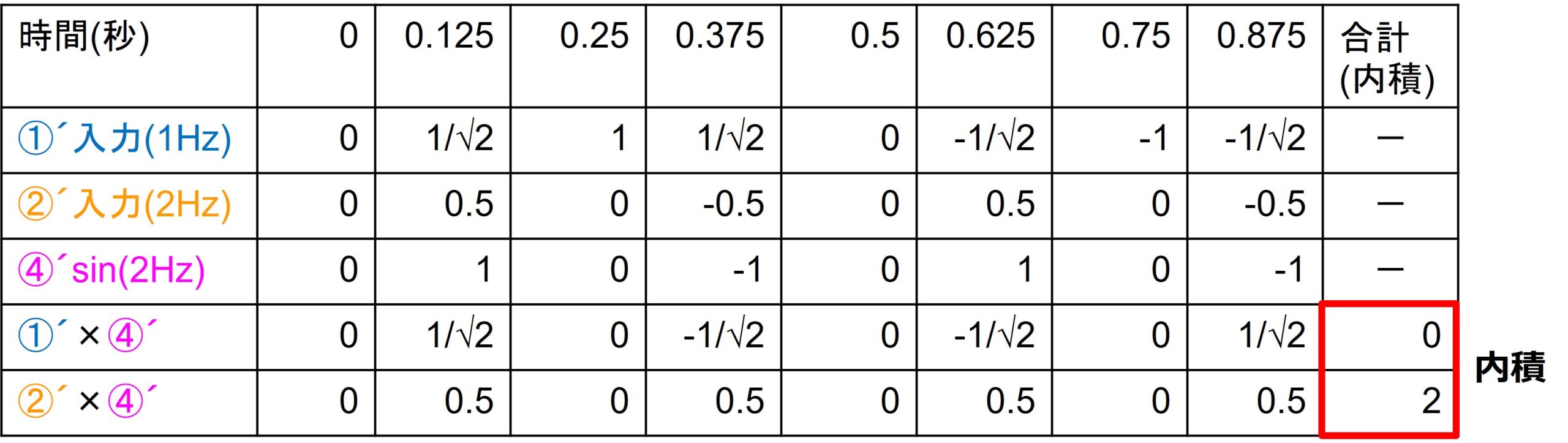
結果、内積が求められました。周波数2Hzの信号をsin2Hzで成分検出できました。cosでは検出できない信号成分はsinで検出できるのです。
cos+sinの組み合わせでさまざまな信号を検出!
さて、前回と今回の記事を通じてお伝えしたかったのは、直交性を持つcosとsinの三角関数のセットでさまざまな波の成分検出ができる。という事でした。
いかがでしたでしょうか?
ちなみに、この方式は検出する信号毎にcos成分とsin成分それぞれの計算結果を使わなければならないので扱いが面倒です。なので効率性を重視することが好きな私としては、普段もっと扱いが楽な方法で計算しています。
次回以降では、オイラーの公式や複素数を用いた、実用的な計算方法についてお伝えしていきますね。
コメント
この記事へのコメントの受付は締め切りました。