1 アナログ回路教室

今回は「PLL（その３）」です。

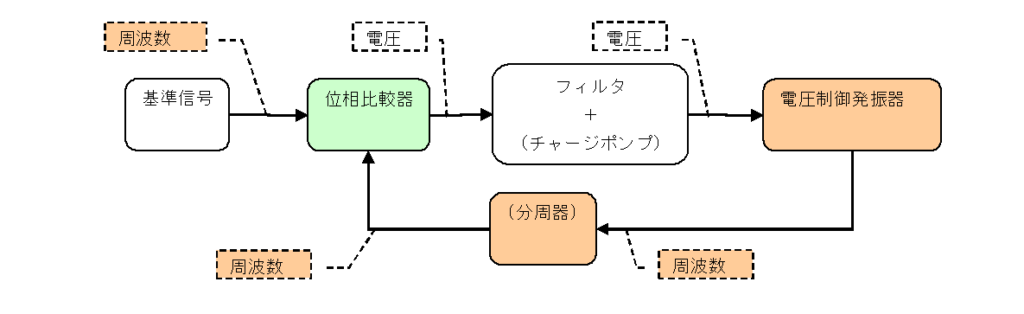
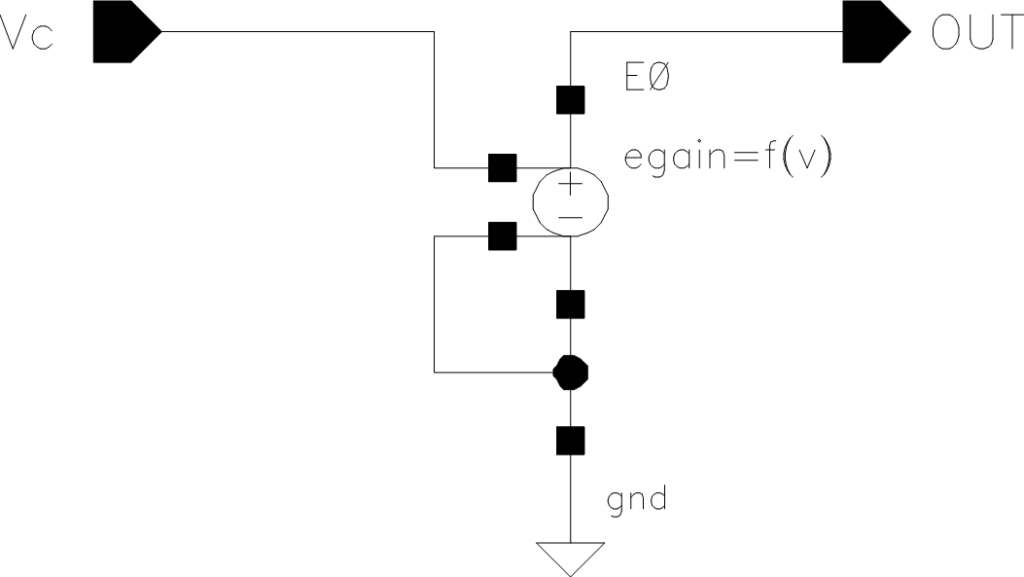
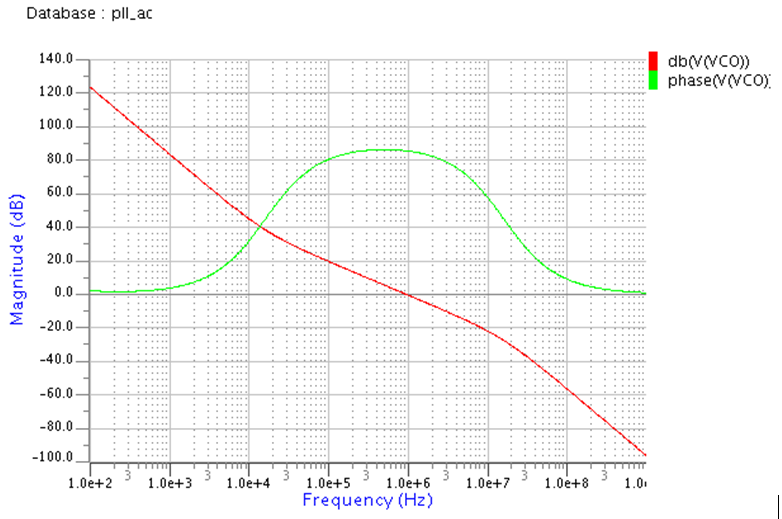
前回はパーツ（位相比較器、VCO）をビヘイビアモデルでモデル化し、PLL全体の周波数特性や過渡解析の例を紹介しました。

今回は、PLL特有に問題（キャプチャーレンジなど）に振れたいと思います。

実験室で”PLLがロックしない”といった叫びを聴いたことがあるでしょうか？僕は何度も叫びました。

では、なぜPLLがロックできないかと言うとそれば「位相比較器に入力される2つに信号の周波数差にフィルタが応答できない」からです。

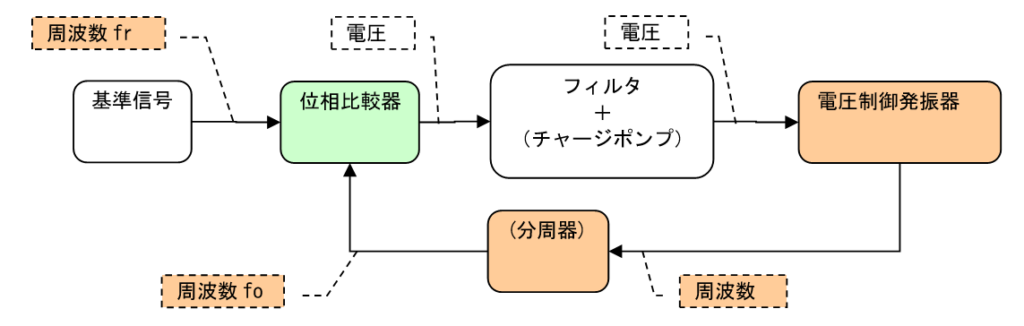
別の言葉で言うと、周波数差がキャプチャーレンジより大きいとPLLは引き込めなくなってしまいます。

PLLに関する文献は山ほどあるので、キャプチャーレンジの計算は文献にまかせて、PLLが引き込めていない時には何が起きているのかを今までのビヘイビアモデルを使って調べてみたいと思います。

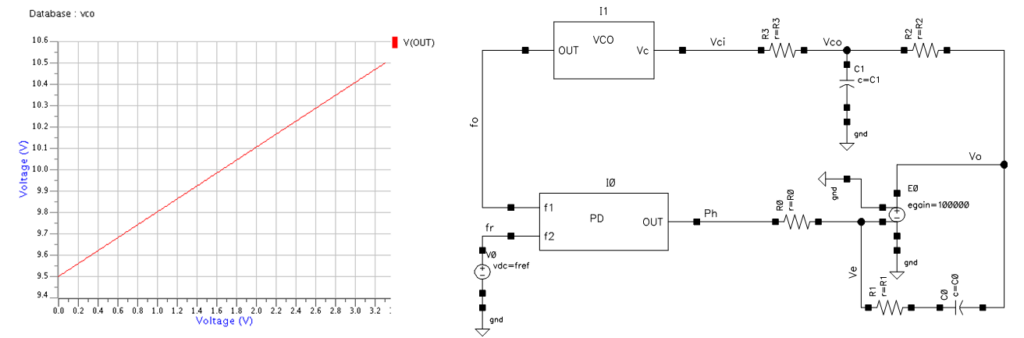
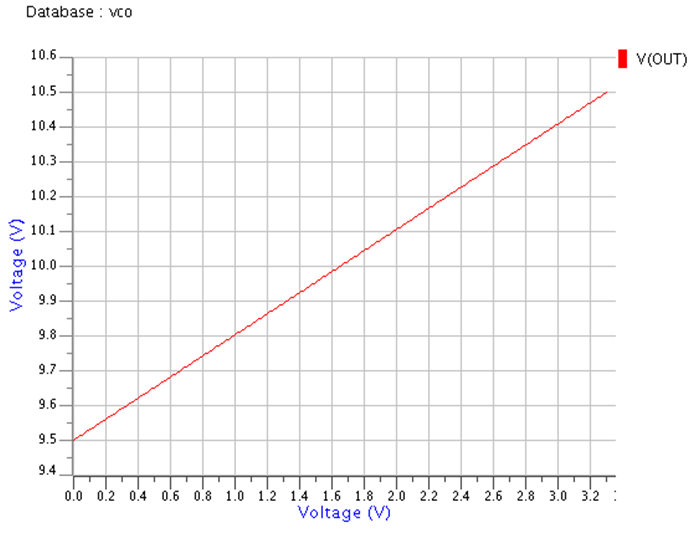
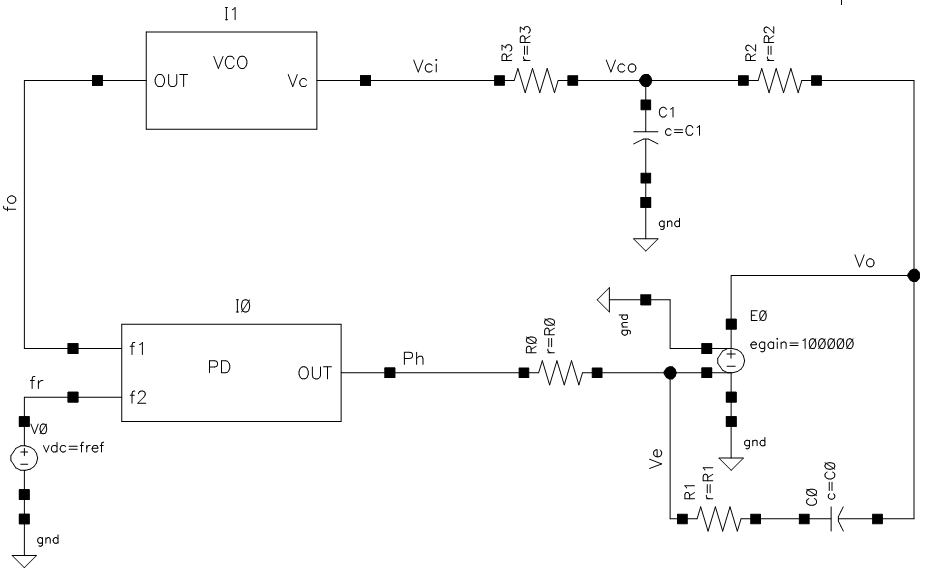
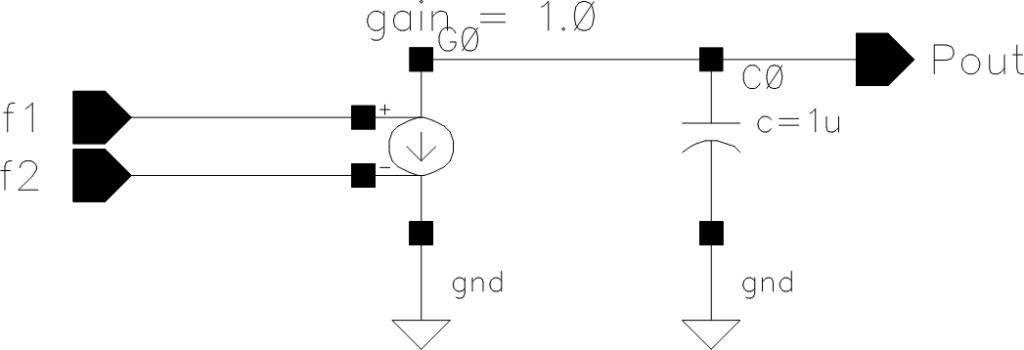
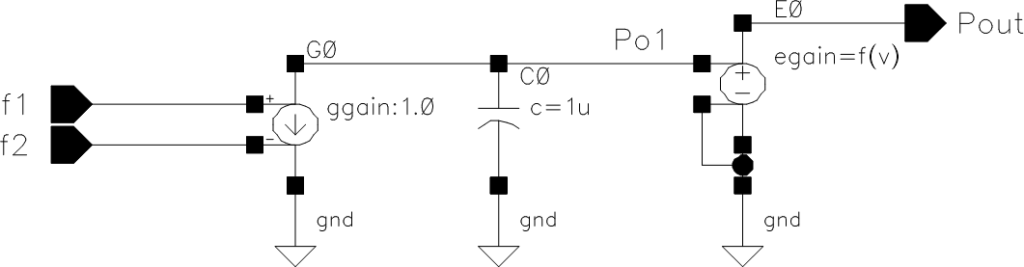
前回のVCOとPLL回路を今回も使います。回路定数も前回と同じで先ずは、

.param r0=510 r1=10k c0=1n r2=1k c1=10pとします。

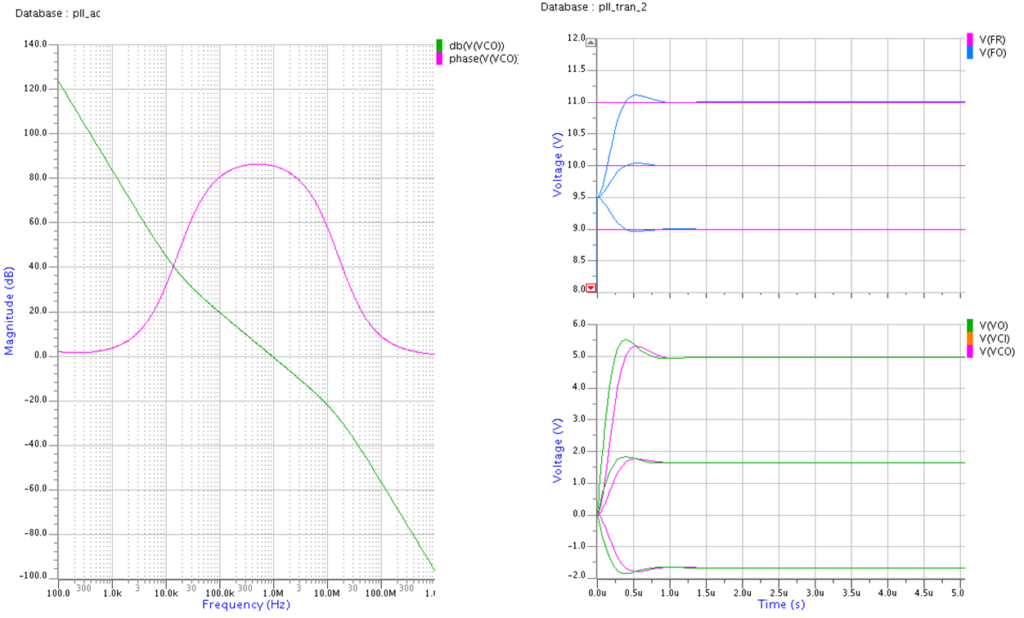
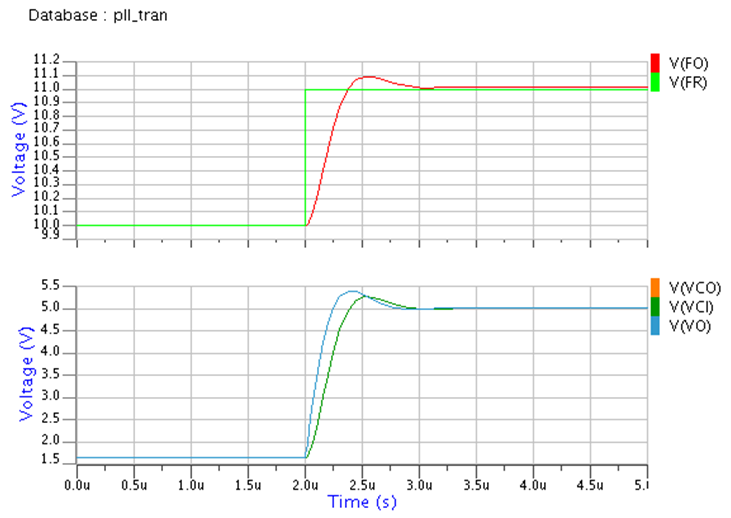
この回路定数だと位相余裕も十分だし、入力する周波数frを9,10,11MHzとした場合のどれでも1.5usec程度で引き込めている事が過渡解析で分かります。

では、フィルタ時定数を変更（注1）してゲイン特性が0dBとなる周波数を1桁遅くした時にどうなるか調べてみると････

注1).param r0=510 r1=1k c0=100n r2=1k c1=100p

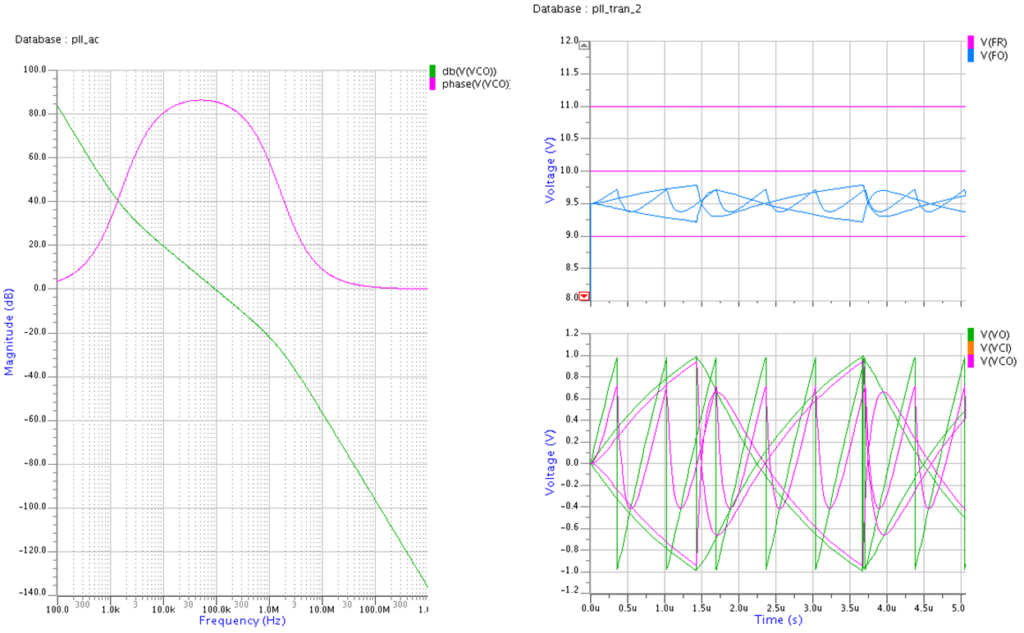
位相余裕などは十分取れているので問題は無いのですが、過渡解析は”PLLがロックしない”と叫んでいます！

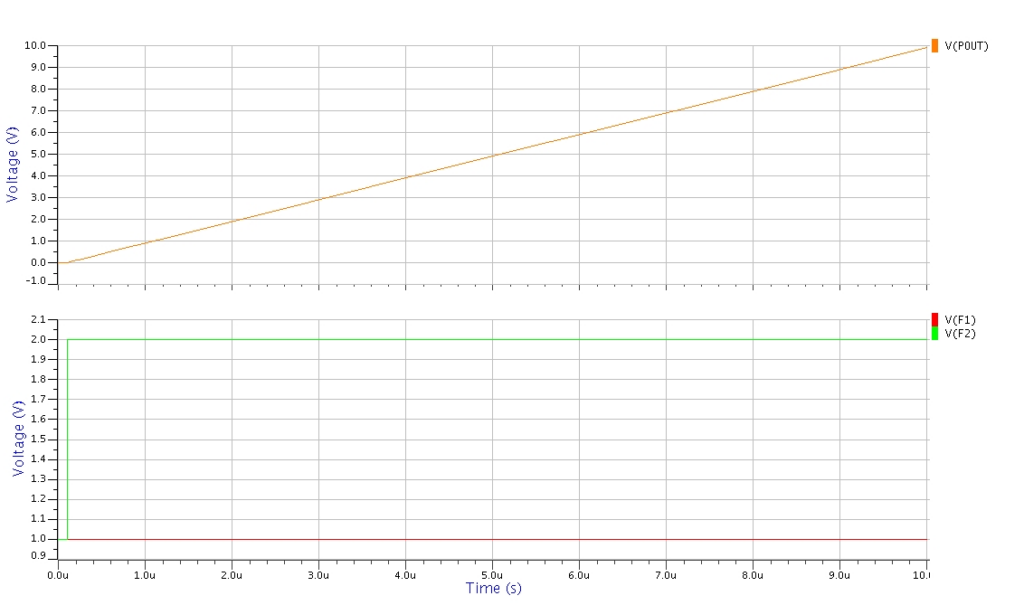
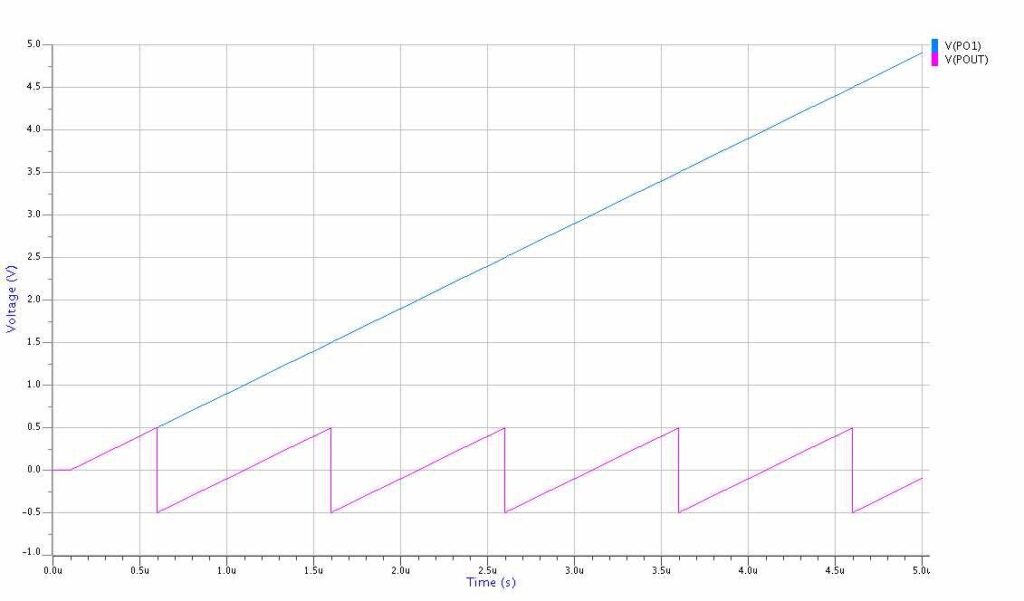
フィルタの時定数を変更したことで、位相比較器のビート信号(差周波数で振動する)をVCOに伝達できず、VCO制御電圧が十分振れずにVCO出力周波数が目標周波数に到達できないために、PLLが引き込めなくなってしまっています。

PLLを使ってジッタを抑圧する時にはPLLの帯域は狭いほう都合がいいので、ゲイン特性が0dBとなる周波数をなるべく低く設定しようとします････そして、上のように罠にはまってしまうのです。

あらゆる電子回路で使われているPLLですが、確実に動く設計をするにはAC解析だけでは不十分で、必ず過渡解析が必要になります。しかし実際の回路をそのまま過渡解析に使っていたら莫大な時間が必要になり、非現実的です。そんな時に便利なビヘイビアモデルを紹介しました。

次回はエミッタ接地やソース接地の増幅器についての予定です。（美斉津）

今回は「PLL（その２）」です。

前回はPLLに不可欠な位相比較器をビヘイビアモデルを使ってモデル化しました。

今回は、電圧制御発振器(VCO)をモデル化してPLL全体の動作を、位相や周波数を分かりやすい電圧に置き換えてPLLを説明してみたいと思います。

PLLは、位相比較器、フィルタ＋チャージポンプ、電圧(または電流)制御発信器、分周器の4つの要素で作る事ができます。

（チャージポンプや分周器はPLLの性能や機能を高めるための回路で、PLLに必須の回路ではありません。）

VCOも位相比較器と同じように1MHz＝1Vと定義して等価モデルを作ります。こちらは、位相比較器より簡単に電圧制御電圧源(VCVS)のみモデル化できます。

.param fo=10

.param dfp=’0.1/3.3′

.param Kv=’1/(2*dfp)’

.param Vref=1.65

e0 out 0 Value=fo*(2/(exp((Vref-v(vc))/Kv)+1))

周波数（１MHｚ）を電圧（1V）で表現すればよいので好みの計算式を入れるだけです。

上の例では自然対数を使って、Vcに1.65Vを与えた時に10MHz（10V）が、Vc＝0～3.3Vと変えると周波数は9.5～10.5MHzと変化するようにパラメータを設定しています（下図参照）。

続いて前回の位相比較器（PC）と合わせて、PLL全体をシミュレーションしてみます。

今回のVCOと前回のPD（位相比較器）をサブサーキットにして、ラグリードフィルタ（R0,R1,C0）と利得100dBの圧縮アンプ（E0）、VCOの制御電圧の雑音除去用に１次のLPF(R2,C1)で構成しています。R3はオープンループ特性などをシミュレーションするときに都合が良いので、入れていますが、実際には0Ωにします。

PDの出力PhもVCOの制御Vciも電圧なので、実際にPLLに使う回路をそのまま使ってシミュレーションが出来るところが都合いいところです。

R3をOPENにしてシミュレーションしたオープンループ特性を上図に示します。利得特性（赤線）が0dBとなる周波数（1MHz）の位相が85°であることから、十分な位相余裕が確保できています。このときの各部品の定数は下記に通りです。

.param r0=510 r1=10k c0=1n

.param r2=1k c1=10p

このままR3をSHORTにして、過渡解析を実施した結果を下図に示します。

2usecでレファレンス周波数（FR）を10MHz => 11MHzと変えたときの過渡解析です。約1uscで安定して収束しています。

PLLは時間に関連する操作をする回路なので理解しにくいし、実際の回路のまま過渡解析をすると時間がかかる嫌な回路なのですが、電圧制御発振器（VCO）と位相比較器（PD）の扱う周波数や位相をビヘイビアモデルで電圧に置き換えることで、解析時間も短くなるし、理解も簡単になると思います。

次回は、PLL特有の特性（ロックレンジやシーズインレンジなど引き込みに関する特性）を今回のモデルを使って説明したいと思います。（美斉津）