
FPGAによる演算高速化の3回目です。今回は演算精度検証と導入効果についてお伝えします。
前回までの記事はこちら。
演算精度検証:評価基準の設定と「EPS Rate」の導入
さて、演算精度の検証は極めて重要な工程です。特に倍精度浮動小数点(64bit)演算を用いる場合、ソフトウェア(Python)とハードウェア(FPGA)では、演算の順序や内部処理の積み上げ方が異なるため、数学的な理由からある程度、数値に微細な差異が生じることは避けられません。
そこで本プロジェクトの評価では、理論的根拠に基づいた「許容範囲(バッファ)」を定義し、その範囲内であれば正当とみなす評価基準を設定しました。
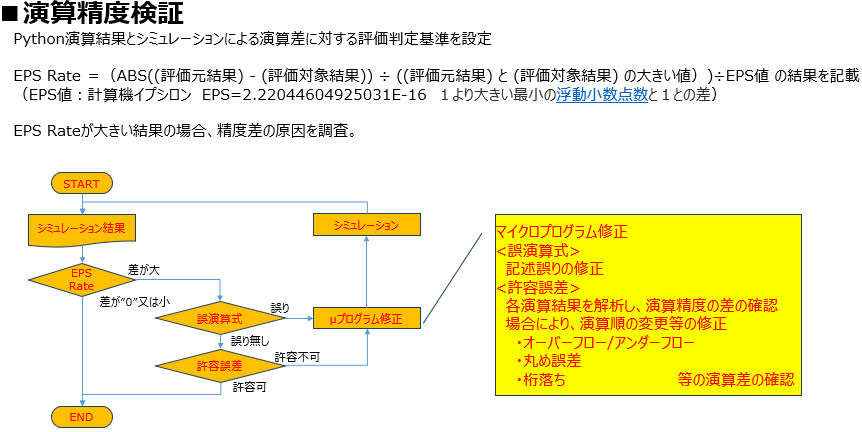
定量的指標としての「EPS Rate」
客観的な評価を行うための指標として、私たちは計算機イプシロンを利用した「EPS Rate」を導入しました。計算機イプシロンとは、「1より大きい最小の数と1との差」を表す値であり、浮動小数点演算における理論的な限界精度を示します。
判定基準は概ね以下の通りです。
- 誤差がEPS Rateの許容範囲内である場合:演算順序の差異や丸め誤差による「数学的に妥当な不一致」と判断し、正当性を承認します。
- 誤差が許容範囲を超える場合:計算式の記述誤り(バグ)や、オーバーフロー、極端な桁落ちなどの「異常な不一致」と判断し、原因究明と修正の対象とします。
論理的考察によるバッファの正当化
Pythonでの演算と、ハードウェアで展開したマイクロプログラムによる逐次演算では、計算の最終結果に僅かな誤差が出るのは自然です。丸め処理や桁落ち等の発生箇所を特定する「考察」を逐次加えることで、誤差が許容範囲内であれば、シミュレーション結果の信頼性を損なわないものであると判断します。
検証フェーズ(1):単体演算モジュールの正当性確認
まず最初は、方程式の計算要素を切り出した「単体演算モジュール」の検証です。ここでは、マイクロプログラム化した演算が、設計図通りに正しくハードウェアリソースを制御できているかを厳密に確認します。
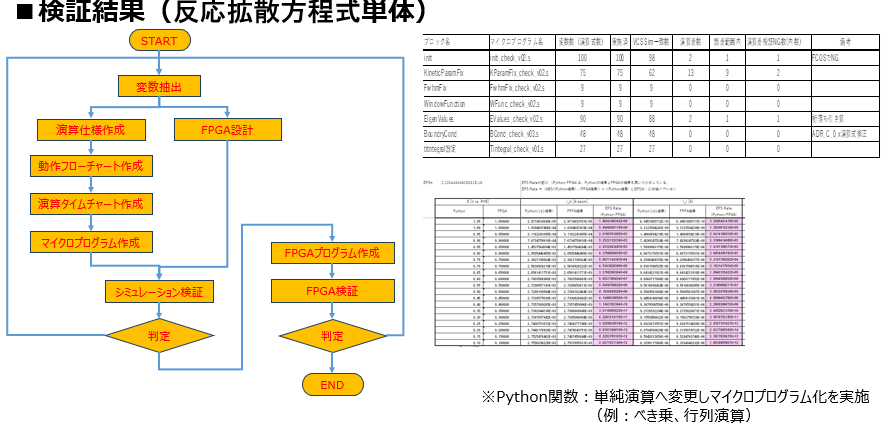
検証フローと実施内容
開発フローに従い、「変数抽出」から「マイクロプログラム作成」、そして「FPGA設計」へと進んだ後、まずはVCSシミュレータを用いた検証を実施します。
この段階では、Pythonで記述された元の関数を、べき乗や行列演算といった「単純演算」に分解した際の論理的な整合性をチェックします。シミュレーション結果とPythonの演算結果を突き合わせ、事前に設定した判定基準に照らして、演算誤差が論理的な許容範囲(バッファ)内に収まっているかを1つずつ判定していきます。単体演算モジュールでの正当性をこのフェーズで確実に担保することが、後続の統合デバッグをスムーズに進めるために必要です。
検証結果の概要:論理的考察による判定
検証詳細データは省略していますが、考察の概要は以下の通りです。
- 整合性の確認: 右の検証結果表にある
initやKineticParamFixといった各演算ブロックで、変数の実働数がVCSシミュレータの値と一致しているかどうかが確認されます。 - 誤差の正当化: 演算結果に差異が生じた箇所(「演算不一致数」としてカウントされたもの)について、大半は「誤差範囲内」として判定されてます。これは、浮動小数点の計算順序の差異などに起因するもので、考察によって妥当と結論づけられたからです。
このように単体演算モジュールの動作がすべて論理的に保証された後、全体系の検証へと進みます。
検証フェーズ(2):全体系プログラムの統合検証
単体演算モジュールの正当性が確認された後、これらを統合して方程式全体の計算を行う「全体系」の検証へと移行します。このフェーズでは、各単体モジュールが正しく連携し、メインプログラムの制御下でシステム全体が期待通りに機能するかを最終確認します。
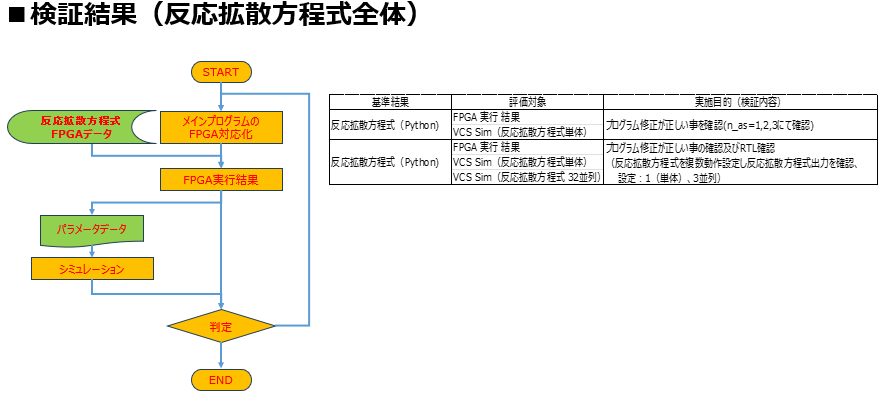
統合検証の具体的なプロセス
統合検証フロー に基づき、実機とシミュレータをクロスチェックする以下の手順を実施しました。
- 実機データの生成: 反応拡散方程式の各演算モジュールで計算された値を、FPGA上のメインプログラムへ投入し、ハードウェア上で演算を実行させます。
- パラメータデータの抽出: FPGA実機での演算結果を「パラメータデータ」として抽出します。
- シミュレータへの再投入と判定: 抽出した実機データを、今度は VCSシミュレータ 側へ投入します。これにより、実機の出力がシミュレータ上の論理動作と完全に整合しているかを直接比較・判定します。
検証により全体プログラムのチェックを行い、必要であれば修正を施し、再度検証プロセスに掛けて、演算結果がソフトウェア上の演算期待値と論理的に合致することを確認します。これらの検証プロセスにより、反応拡散方程式のFPGAハードウェア上の演算結果への信頼性を高めていきます。
ハードウェア化の効果(1):単体実装で38%高速化!
上記2段階の検証を終えた反応拡散方程式のアルゴリズムをFPGAへ実装、差分進化法を実施しました。その結果、従来のソフトウェア(Python)での実行と比較して、顕著な高速化が確認されました。
演算時間の短縮実績

同一の計算条件において演算時間を比較したところ、以下の結果が得られました:
- ソフトウェア(Python): 100時間
- FPGA(反応拡散方程式×1): 62時間
方程式の演算単体のFPGA化として、38%のFPGA達成しました。
さらなる高速化を目指し、余剰リソースを活用して並列処理化
FPGAレイアウト図(左下)は、反応拡散方程式の全体系を1個を実装した時のブロック利用率です。FPGA(Alveo U250)の搭載可能ブロックに対して使用率的にまだ十分な余裕があるため、空き領域へ全体系を複数搭載し並列処理化を検討しました。
ハードウェア化の効果(2):32個並列実装による劇的高速化!
弊社にはFPGA上のプログラムレイアウトが得意なエンジニアが在籍します。本プログラムの並列搭載レイアウト検討を託したところ、全部で32個搭載できることが分かりました。このレイアウトで実装を行い、結果として1個で38%効率化した方程式演算を、32回同時並列処理するまでの、高速演算環境を実現することができました。
驚異的な演算時間の短縮
32個 並列実装を施したFPGAで検証した結果、全体の演算時間は以下のように劇的な変化を遂げました:
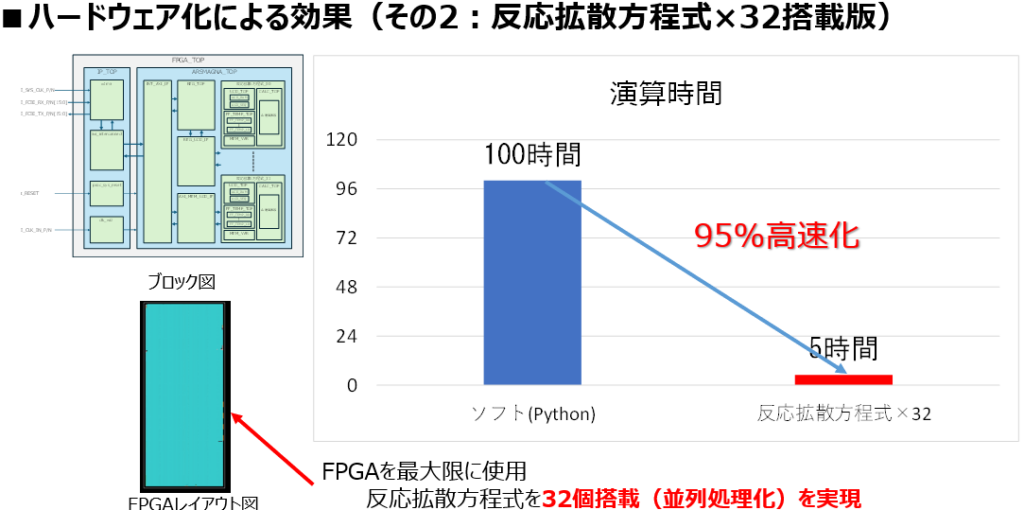
- ソフトウェア(Python): 100時間
- FPGA(反応拡散方程式×32): 5時間
FPGAレイアウト図を見ると、単体実装時とは対照的に、FPGAの領域が隙間なく埋め尽くされていることがわかります。
最終的に、ソフトウェア演算に比較して、95%もの演算時間削減に成功。32種類の異なるパラメータセットをそれぞれの演算ユニットへ投入し、並列に解を抽出することで、差分進化法の探索スピードを極限まで高めることができました。
まとめ:計算の「壁」を突破し、さまざまな現場の数理最適化へ
今回の開発では、反応拡散方程式を「差分進化法」という数理最適化のプロセスに組み込み、従来100時間を要したシミュレーションを5時間まで短縮することに成功しました。
【今回のプロジェクトのポイント】
- 超効率のFPGAプログラムレイアウト: Alveo U250の演算能力を限界まで引き出し、32個の反応拡散方程式ユニットを詰め込みんだ。
- 並列処理の実現と差分進化へのフィードバック: 各ユニットが独立して計算を行い、その結果を「差分進化法」のプロセスへ高速にフィードバックする仕組みを構築した。
- 圧倒的な高速化:結果としてこれまで4日間以上要していた複雑なパラメータ探索がわずか5時間で完了。研究・開発の全体サイクルを大幅に改善。
(参考)学術・産業の「計算課題」を解決するD-Clueのソリューション
今回のような、ソフトウェア演算をマイクロプログラム化し、FPGAハードウェアアクセラレータへ実装する開発フローは、極めて高い汎用性を備えています。素材研究や、ビジネスにおける複雑な意志決定プロセス等のアルゴリズムが数理モデルで定義されていれば、様々な最適化フローを高速処理することが可能です。
弊社では、お客様が直面する数理最適化の演算高速化に対し、FPGAの特性を最大限に活かして以下のサービスを提供しています。
- 差分進化法・その他の数理最適化: 今回のプロジェクトでも活用された、複雑なパラメータ探索や数理モデルの高速化を支援します。 FPGAハードウェアアクセラレータ:N Program
- 組み合わせ最適化: 物流のルート最適化、工場のシフト作成、製造工程の効率化など、膨大な組み合わせの中から最適解を導き出します。 FPGA疑似量子アニーリング:Qalmo
FPGAハードウェアアクセラレータで、数理最適化演算における「時間の壁」を取り払い、研究開発やビジネスのスピードを次なる次元へと引き上げていく。ディー・クルー・テクノロジーズは、これからも「演算スピード」が創り出す新しい価値にこだわって挑戦し続けます。