反射の周波数特性と波形

Sパラメータと反射

今回もSパラメータについてもう少し紹介したいと思います。

S11が入力側（左側）の反射量を示すなら、S22は出力側（右側）の反射量を示します。

そしてS21が入力から出力への（左から右への）電力伝達量を、S12は出力から入力への(右から左への)電力伝達量を示します。

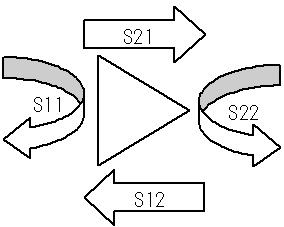
Sパラメータの中で先ず注目するのは、S21ではないでしょうか。

Sパラメータで、LSIの内部波形を推定できる

非測定物の周波数特性がどうなっているか、ピーキングは無いか？　などを先ず確認する時に使います。そして次に注目するのがS11やS22ではないかと思います。 S11やS22に注目する理由は、実際に触ることが出来ないLSIの内部の波形を推定すること出来るからではないでしょうか。

寄生素子の影響を特定する手助けとなるSパラメータ

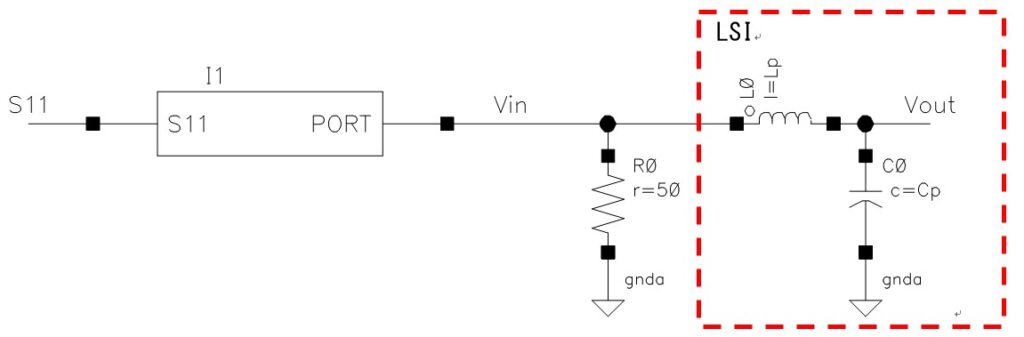
例えば、実際の評価でなぜかエラーを発生してしまうLSIがあったとします。寄生素子の影響であることはなんとなくわかっているのですが、どう調べたら良いか分からないこともあると思います。そんな時、S11が原因究明の手助けになってくれます。

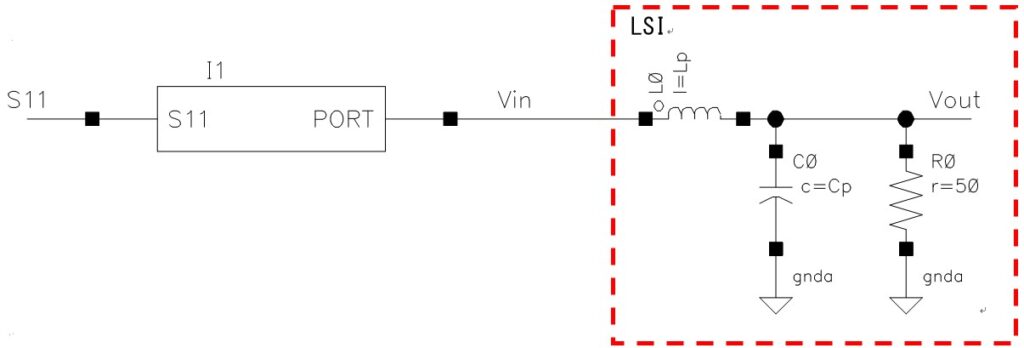
まずLSIの等価モデルを想定します。上の図の様に最も簡単なものを使い、インダクタL0はボンディングワイヤーを、コンデンサC0はPADと入力トランジスタの寄生容量を等価するものとします。

PAD容量や入力トランジスタの寄生容量はデバイスの特性なので、デザインマニュアルなどを参照すればある程度の数字を得ることができると思います。問題なのはインダクタで、ボンディングワイヤーの長さ（特にループになっている分）や、PKGの端子がどの程度のインダクタになっているかを知るには骨が折れます。

S11からエラー原因が特定されない

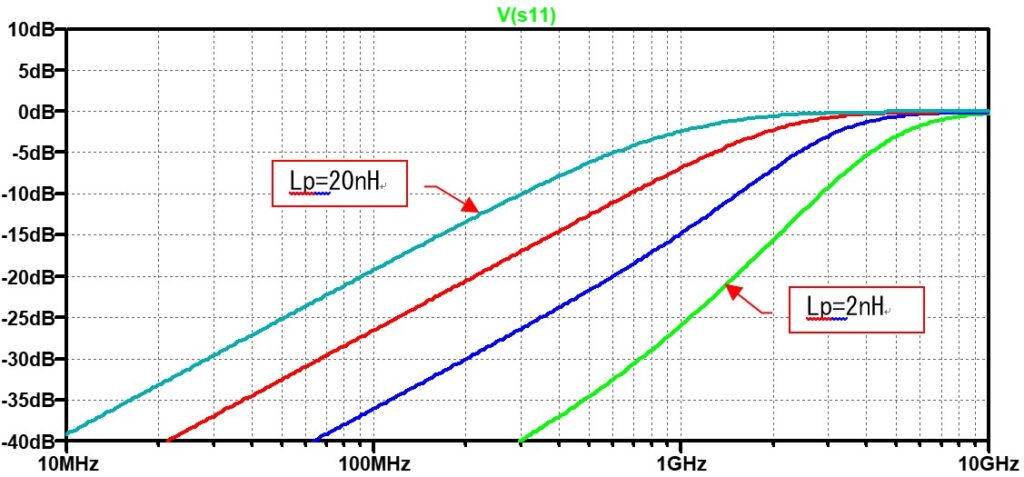
上の回路で、Cp=1pFとしてインダクタLpを変化（2n, 5n,10n,20nH）させたときのS11を計算した結果を下に示します。

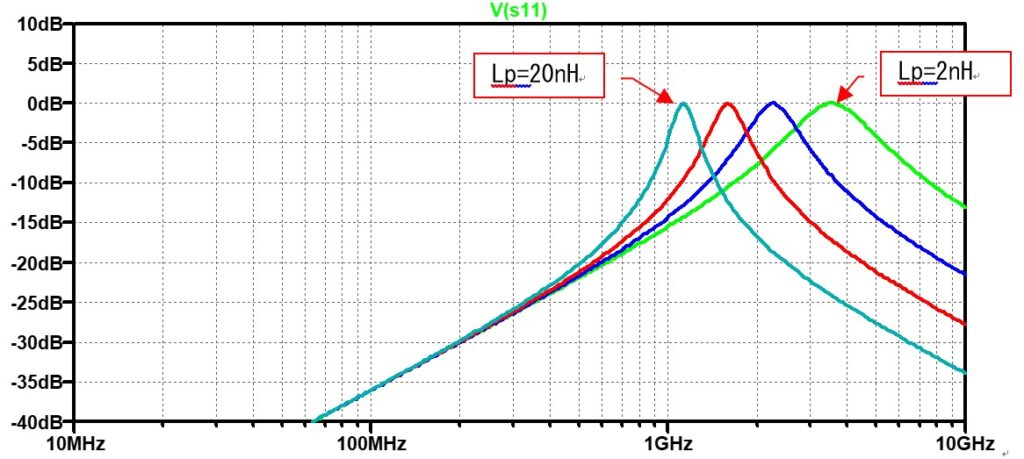
等価回路を良く見ると、L/Cの直列共振回路となっています。なので、共振周波数では整合抵抗R0に非常に低いインピーダンスが並列に入っている事に成ります。そのためS11は全反射（入力した電力の全てを反射する）し0dBを示す事に成ります。もし、実測したS11に全反射となる周波数があれば、その周波数を合わせるようにインダクタを計算して求めることが出来ます。 しかし、S11が全反射する周波数から寄生インダクタを求めても、なぜエラーが発生するかの説明は出来ません。そこで、等価回路のVout端子の周波数特性を確認してみます。

等価回路のVout端子の周波数特性を確認する

S11の全反射する周波数で、ピーキングが発生していることが分かります。

入力波形にはリンギングが表れないことがある

このまま過渡解析をしてみると・・・

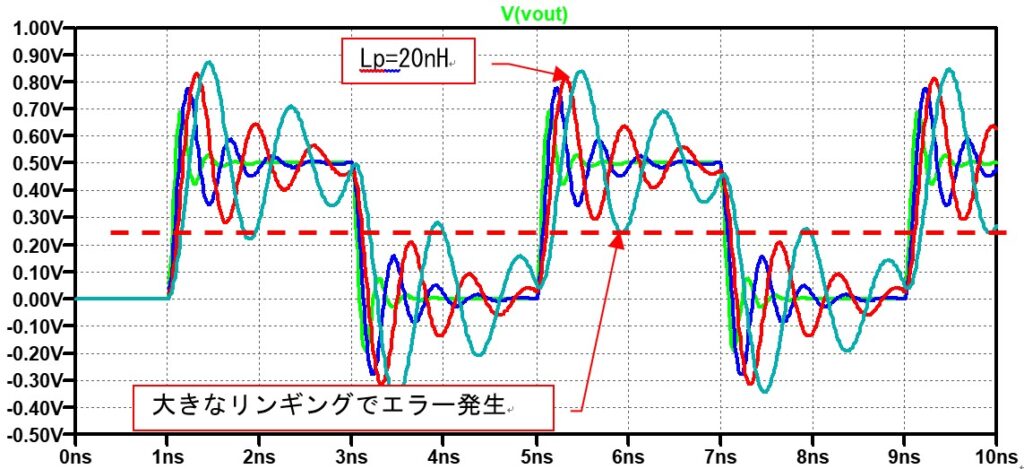
大きなリンギングが発生して、エラーになっていることが分かります。更に厄介なことはLSIの入力波形を見ると分かります。

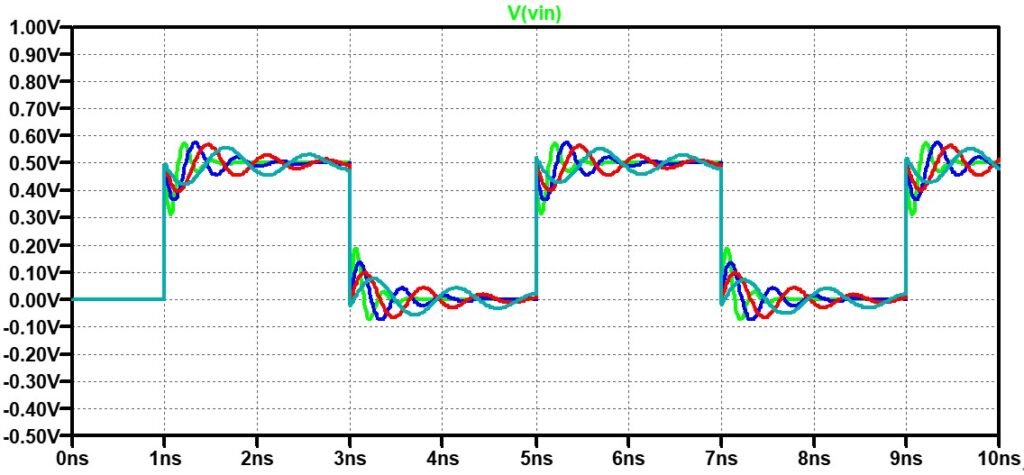
LSIの入力波形には大きなリンギングは現れていません！

つまり、このLSIを評価するときに、LSIの端子Vinをプローブで観測しても上の図の様に“少しリンギングが有るけど、エラーするほどではないので、入力部には問題はない”と済ましてしまうと、永遠にエラーするなぞが分からないままになってしまいます。

入力部とSパラメータの測定結果比較が重要

簡易的でも、入力部の等価モデルとS11の測定結果を比較することで、実測できない内部の波形を推定することが出来ます。 ところで、LVDSなどの高速インターフェースでは整合抵抗をLSIの中に搭載することが一般的です。上の回路例では、整合抵抗R0はLSIの外部に実装していますがこれをLSI内に移動した場合の効果はと言うと・・・

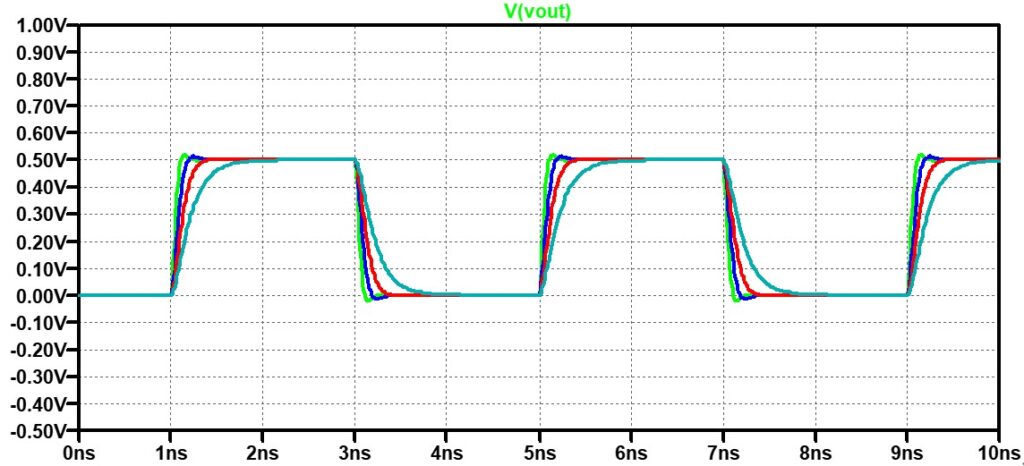
その効果が圧倒的なのは波形（図5が外部整合、図9が内部整合）を見れば一目瞭然です。

整合抵抗（終端抵抗）は偉い

インピーダンス整合用の抵抗R0は、終端抵抗とも呼びます。そこ場所で今までの伝送路が終わるのでこの名前なのだと思うのですが、やはり終端抵抗は最後につけないとその効果が出ないと言うことだといってしまえばそうなのですが・・・寄生容量やインダクタや伝送路のミスマッチ、歪を全て背負って、終端する抵抗って偉いと思うのです。

次回はこのSパラメータと他のパラメータの関係について紹介していきたいと思います。

---