さあ、今日は複素正弦波を使って具体的に離散フーリエ変換の計算の仕方をお伝えします。

離散フーリエ変換の公式

再び、離散フーリエ変換の公式です。

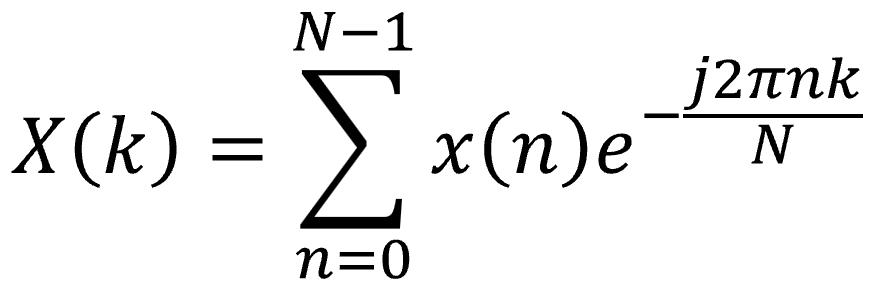
左辺のX(k)は、ある周期の波kに対し計算実施した結果で、全部でN個分のデータとなります。

右辺のx(n)は、”0～N-1の離散フーリエ変換対象の信号”です。 このブログではx(n)を”時刻 0～N-1の時間信号”のイメージで計算してましたが、実際は時刻に限らず、等間隔に並んだ離散信号なら何でもよいのでこの表現がしっくりきます。右辺の計算は、たとえばNが8であれば、”0から7までの８個の離散フーリエ変換対象の信号”に、複素正弦波（この公式では便宜上指数に-が付きますが内積計算に影響ありません）を乗じて各信号との内積を求め、それらをΣ(合計)することを意味します。

離散フーリエ変換公式による計算

N=8の時を例として計算方法をお伝えします。

k=０の時、各要素の計算はこんな感じになります。各要素は複素数になるので、複素平面上の円回転でも表現できます。視覚的に理解いただくために要素の下に掲載しました。

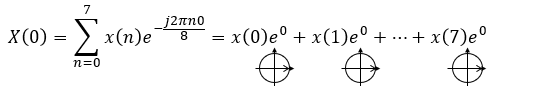
こんな感じになります。ちなみにX(0)のときはeの指数部が常に0になります。

次に他の7個分を計算します。kの値を変えるとこのとおり、回転速度が変わります。どう変わるのか視覚的に示すために複素平面図に矢印で示してみました。一部省略しましたが、kを0→7まで増やしていくとこんな感じになります。

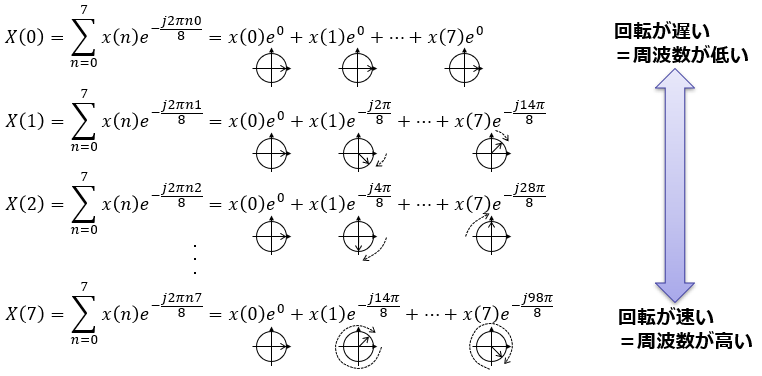
ここで最もお伝えたいことは、kの値が低いほど回転が遅く、周波数も低くなることと、逆にkの値が高いほど回転も速く、周波数は高くなるということです。

三角関数を使わない、シンプルな離散フーリエ変換の計算テクニックとは、このように分析対象の波に対して、低い周波数から少しずつ高いものにずらして複素正弦波との内積を取る。その計算結果から周波数成分を見つけていくというアプローチになります。

私の離散フーリエ変換の公式を使った計算テクニックとは以上のようなものですが、いかがでしたでしょうか？ このブログ全体を通じてディジタル信号処理や離散フーリエ変換について皆さまの関心が高まったり、ご理解が深まれば、大変嬉しく思います。

最後に、信号処理ついてご質問やご相談がありましたら、下記相談フォームにて承ります。信号処理の利活用方法、技術応用による性能UPなど、遠慮なくお伝えください。